MRtrix3教程 #1 快速入门
- 相关知识点
- 基础概念
- MRtrix Viewer使用
- BTC_preop（Brain Tumor Connectomics Data）数据下载
- MRtrix数据格式与格式转换
- 检查Bvals和Bvecs
- 学习参考
MRtrix是一个用于分析扩散数据的软件包。与张量拟合技术相比，MRtrix的一个显著优势是他们的约束球面反卷积方法，或称CSD(Constrained spherical deconvolution)；该方法将每个体素的扩散信号解卷为一系列重叠的纤维束,这就减少了在拟合张量时可能出现的纤维交叉问题。
除了MRtrix团队创建的命令库之外，该软件封装了FSL的部分命令：特别是topup和eddy这两个命令。如果你还没有安装FSL软件，请下载并安装fMRI软件包FSL。
相关知识点
- 学习使用fixel-based分析方法来量化每个体素的白质纤维密度
- 学习怎么使用概率纤维束成像创建纤维束图
- 学习如何创建连接体(connectomes)以及如何可视化连接不同大脑区域的纤维数量
基础概念
1. T1像与T2像
在T1或解剖扫描中，白质比灰质浅，而灰质又比脑脊液浅；在T2或功能扫描中，相对强度被翻转。
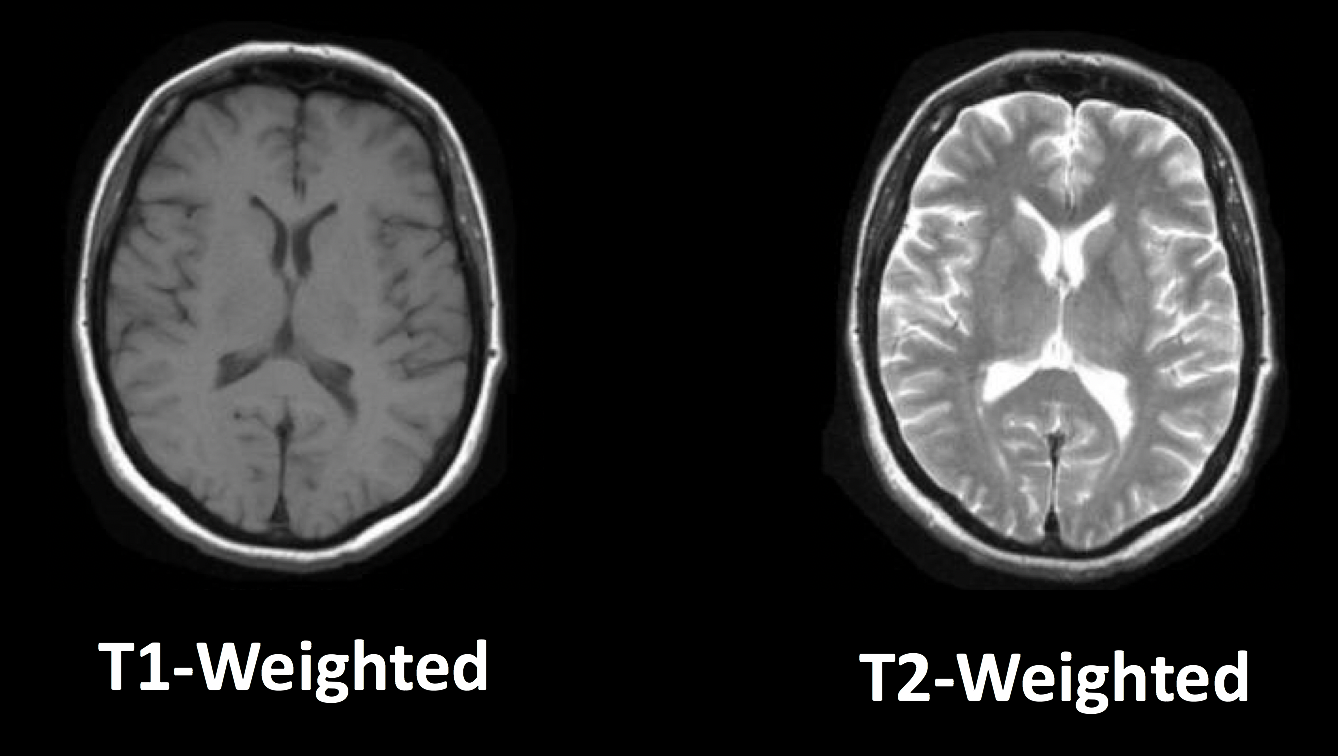典型的T1加权（解剖）和 T2加权（功能）图像。注意从T1加权成像到T2加权成像时组织类型的相对强度是如何反转的。
然而，还有其他类型的图像可以通过MRI扫描仪获得。在本节中，我们将重点讨论扩散加权核磁共振成像，或称dMRI，它测量大脑不同部位的相对扩散性–特别是在白质束内。
2. 白质的结构
为什么dMRI会关注白质束？想象一下剥开一根奶酪条，然后想象一下剥开大脑–就像奶酪条一样，大脑有首选的撕裂方向。这些方向与底层白质束相对应，白质束是厚厚的有髓神经元束（myelinated neurons），连接着大脑的附近和遥远的部分。例如，下纵束(inferior longitudinal fasciculus)连接大脑的视觉和颞部区域，而钩束(uncinate fasciculus)则连接大脑的颞部和下额部。这些神经束沿着大脑的所有三个维度行进，它们可能相互平行或相互交叉。
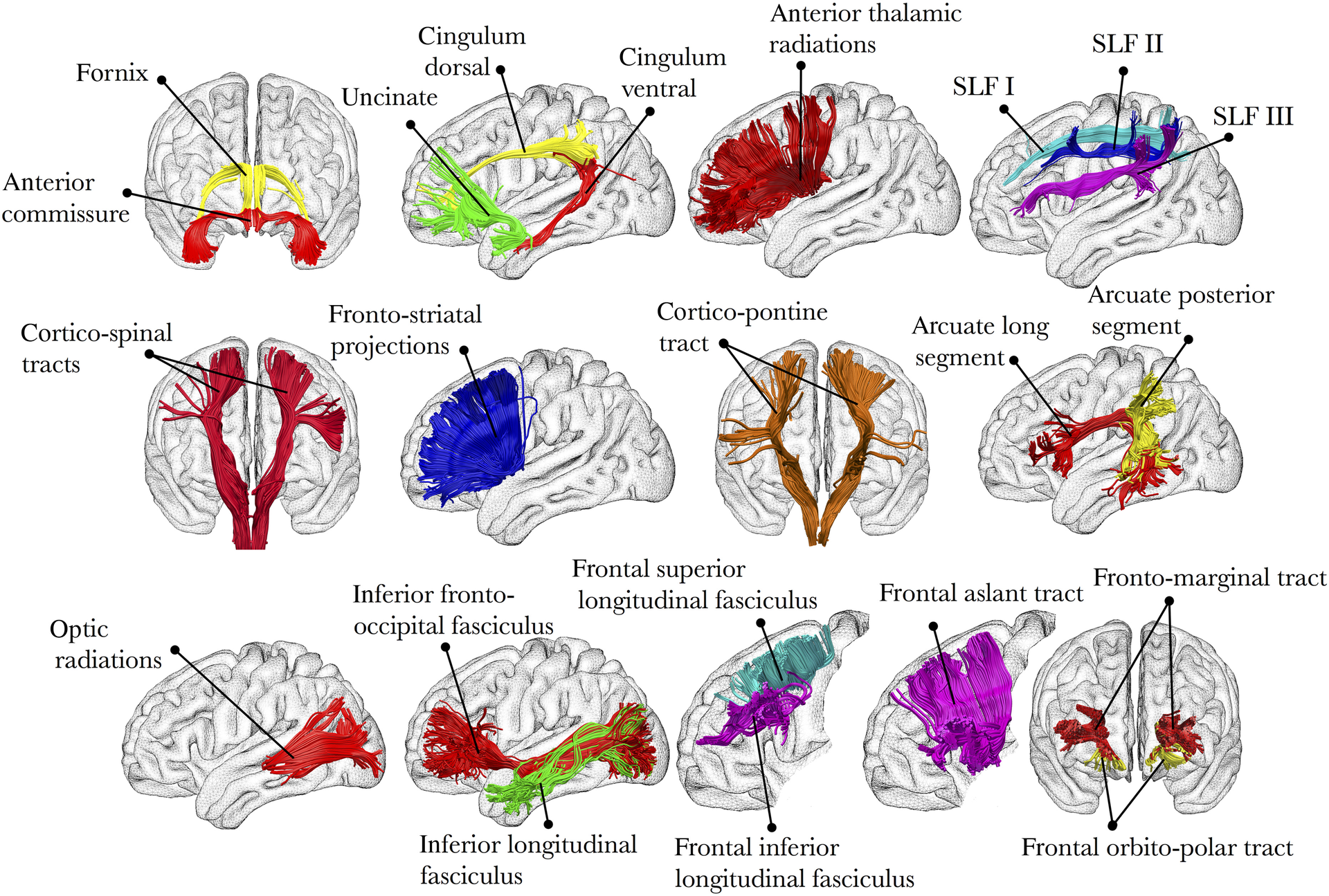Illustration of several main white matter tracts. Figure taken from Thiebaut et al., 2015.
大脑的白质因其颜色而得名；这些神经元是高度髓鞘化的，这意味着它们有一层厚厚的脂质涂层，既能使它们绝缘，又有助于电脉冲的传输，就像绝缘的电线。相比之下，灰质神经元则相对没有髓鞘，这使得特定区域内的神经元密度更高。
3.扩散梯度（Diffusion Gradient）与B值（B-value）
扩散梯度由以下参数生成：
- The magnitude of diffusion gradient (G);
- The time between gradients (𝚫) ;
- T duration of diffusion gradient (𝜹).
这些可以组合成一个方程式，即所谓的b值，如下图所示。
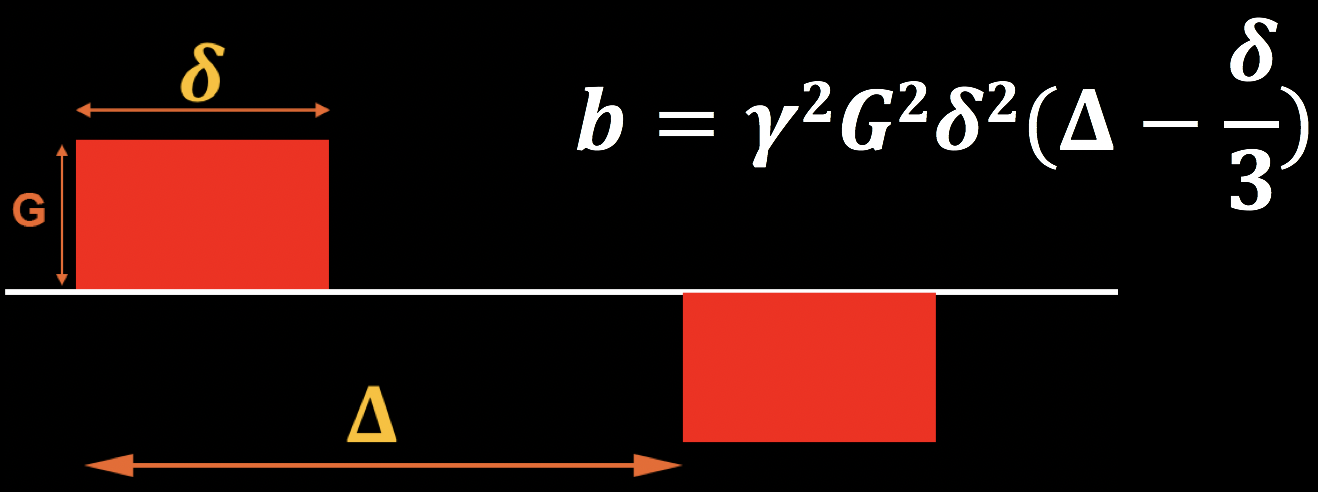
请注意，b值与梯度的大小、梯度的持续时间和梯度之间的时间成正比；如果这些参数中的任何一个增加，b值也会随之增加。
下图所示b值为0的扩散加权图像与典型的T2加权图像几乎相同–脑脊液（CSF）是亮的，灰质是暗的。当我们增加b值时，我们看到在大脑的特定部位，主要是白质内有更大的信号损失。这是因为这些白质束内的水主要沿着束的方向扩散，生成的图像显示出相应的低信号。(较高的b值也使图像更容易受到图像伪影的影响，如运动和被称为涡流（eddy）的磁流）。
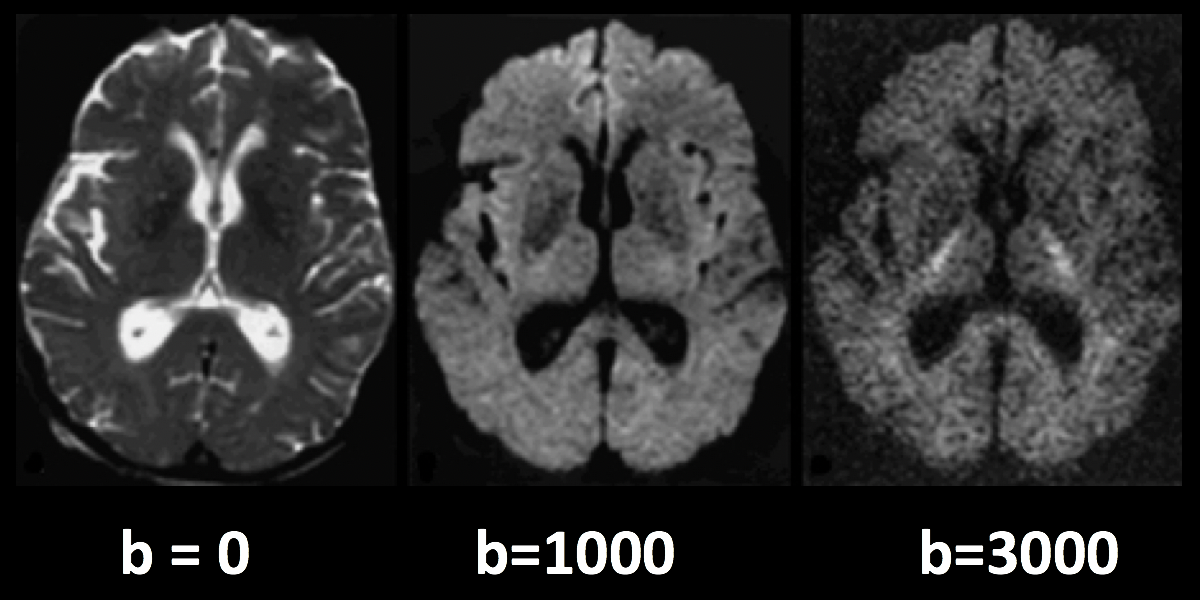较高的b值将对检测扩散更敏感，但存在更多噪声和更易受振动伪影影响的风险。
以一个以上的b值获取的扩散图像被称为多壳获取(multi-shell acquisitions)。这可以对扩散的方向进行更精细的区分。因为根据扩散量，图像将在每个 b 值处显示不同量的信号损失。
4.B向量（B-vectors）
到目前为止，我们已经学会了如何应用扩散梯度，以及如何解释图像中产生的信号。为了完善我们对扩散图像如何产生的理解，我们还需要知道应用梯度的方向。这些方向被称为b-vectors，或简称bvecs。你会注意到，一旦下载了扩散加权扫描的数据，会有两个文本文件–一个通常有后缀**.bval**，表示b值，另一个有后缀**.bvec**，代表b向量。
假设收集了40张扩散加权图像，且第一个volume的b值为0，其余volume的b值为1000。bvals文件将有40个条目，每个bval对应于扩散加权图像中的一个独立容积。另一方面，bvecs文件将有40个三元组数字，表示该volume在X、Y和Z方向的扩散梯度方向。如果我们知道梯度的方向和大小，我们可以根据从这些体素获得的信号的变化，对沿梯度的扩散进行有根据的猜测。
0 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 0
0 0.98807364702224 0.01873399689793 0.10248889029026 -0.60841137170791 0.11875726282596 0.83128935098648 0.8792484998703 0.29209038615226 0.97650814056396 -0.45731022953987 -0.26519000530242 -0.34403458237648 0.3694197833538 -0.5363900065422 0.69562232494354 0.79384189844131 -0.8140320777893 -0.15647158026695 -0.05976745858788 -0.8508283495903 0.54968833923339 -0.86733847856521 -0.96609008312225 0.33223336935043 0.17501354217529 -0.22683978080749 -0.78282612562179 -0.01112493406981 -0.23269833624363 0.91476505994796 -0.67205339670181 -0.23402217030525 0.4485667347908 0.18897378444671 0.94987839460372 -0.9148513674736 -0.44173404574394 -0.73895621299743 0.79589116573333 -0.57393205165863 0.60627329349517 0.05053876712918 -0.64032816886901 -0.00203162245452 -0.65047174692153 -0.05030425265431 0.52077239751815 -0.77435040473938 -0.46209508180618 -0.31149512529373 0.72376120090484 0.35057383775711 0.58841001987457 0.30768102407455 0.58442068099975 -0.43342873454093 0.60935580730438 0.21404276788234 -0.14940990507602 -0.08567165583372 -0.44128519296646 -0.42076206207275 0.77442812919616 0.26836225390434 -0.9886794090271 -0.01840304397046 -0.10154163837432 0.60881024599075 -0.11891078948974 -0.83279365301132 -0.87748628854751 -0.2911439538002 -0.97587263584137 0.45687541365623 0.2644036412239 0.34314483404159 -0.37085926532745 0.53519117832183 -0.69378554821014 -0.79480296373367 0.8121600151062 0.15640883147716 0.0600587055087 0.852090716362 -0.54919642210006 0.86885839700698 0.96635591983795 -0.33167579770088 -0.17399430274963 0.22716110944747 0.78298610448837 0.01114399824291 0.23385895788669 -0.91456174850463 0.6740972995758 0.23286212980747 -0.44666454195976 -0.18938872218132 -0.95080780982971 0.91358888149261 0.44201084971427 0.73829895257949 -0.79423487186431 0.5715285539627 -0.60760217905044 -0.05102515220642 0.63832122087478 0.00161422998644 0.65151822566986 0.05034917593002 -0.52154493331909 0.77315002679824 0.46328803896904 0.31260219216346 -0.72411864995956 -0.35144120454788 -0.58741247653961 -0.3066479563713 -0.58275157213211 0.43335115909576 -0.61113619804382 -0.21487313508987 0.15031689405441 0.08529827743768 0.43970343470573 0.42256951332092 -0.77373939752578 -0.26831793785095 0
0 -0.01852251589298 0.99980324506759 0.65190172195434 0.77669501304626 0.51643615961074 0.24059402942657 0.11685247719287 0.9260526895523 0.1235506683588 0.85478085279464 0.85505563020706 0.64182126522064 0.37680619955062 0.68586140871048 0.09719203412532 0.50450026988983 0.05807575210928 0.54915863275528 0.96547383069992 0.4169929921627 0.83072793483734 0.1662128418684 0.24979101121425 0.7805278301239 0.19109116494655 0.95903354883194 0.61787110567092 0.36186653375625 0.73179537057876 0.40054687857627 0.23983028531074 0.15332546830177 0.19694779813289 0.11983390152454 0.24672436714172 0.22436074912548 0.89713984727859 0.64289963245391 0.39663499593734 0.03941979259252 0.51400256156921 0.72016698122024 0.40433484315872 0.82592779397964 0.60496312379837 0.3299603164196 0.7809572815895 0.47501924633979 0.56527525186538 0.39308729767799 0.67895883321762 0.67152732610702 0.68220138549804 0.50802809000015 0.41673135757446 0.81480491161346 0.23104956746101 0.87857925891876 0.07421392202377 0.90127205848693 0.31627905368804 0.14664776623249 0.59513312578201 0.95450747013092 0.01850401610136 -0.99982780218124 -0.64990043640136 -0.7771503329277 -0.51860928535461 -0.24067203700542 -0.11694828420877 -0.92531460523605 -0.12353691458702 -0.85404860973358 -0.85365968942642 -0.6399946808815 -0.37781903147697 -0.68439275026321 -0.0959820151329 -0.50524860620498 -0.05786505714058 -0.5474424958229 -0.96439582109451 -0.41736420989036 -0.83053159713745 -0.16672849655151 -0.24981169402599 -0.77884089946746 -0.18985091149807 -0.95970767736435 -0.61819595098495 -0.36017289757728 -0.7332512140274 -0.40044379234314 -0.24039900302887 -0.15302035212516 -0.19559489190578 -0.12080664187669 -0.24619971215725 -0.22405302524566 -0.89700889587402 -0.64234739542007 -0.39595165848732 -0.03925511986017 -0.51513165235519 -0.72206115722656 -0.40336072444915 -0.82375878095626 -0.60597515106201 -0.33166021108627 -0.78185319900512 -0.47429451346397 -0.56685864925384 -0.39410242438316 -0.67933368682861 -0.67376309633255 -0.68098336458206 -0.50633686780929 -0.41543397307395 -0.81643337011337 -0.23181574046611 -0.87980186939239 -0.07386588305234 -0.9025894999504 -0.31557491421699 -0.14773198962211 -0.59484159946441 -0.95507723093032 0
0 -0.15286396443843 -0.00651476159691 0.75134563446044 -0.16303530335426 -0.84805089235305 -0.50107139348983 0.46180909872055 0.23897625505924 0.17654202878475 0.24539165198803 0.44559413194656 0.68535083532333 -0.849438726902 0.49181297421455 0.71180284023284 -0.33955046534538 0.57790917158126 0.82093930244445 0.25355103611946 -0.31969979405403 0.08794292062521 -0.4691452383995 -0.06537938863039 0.529525578022 0.96584397554397 -0.16970072686672 -0.07361198216676 0.93216359615325 -0.64056777954101 0.05260347947478 -0.7005894780159 0.96006506681442 0.87177950143814 -0.97464287281036 -0.19198505580425 0.33572205901145 -0.00334380893036 0.2015535980463 0.45742538571357 0.81795364618301 -0.60682290792465 -0.69195765256881 0.65306454896926 0.56377238035202 -0.45924523472786 -0.94265359640121 -0.34482169151306 0.41801697015762 -0.68332421779632 -0.86513191461563 -0.12322624027729 -0.65280097723007 0.43402189016342 0.80451220273971 0.69626688957214 -0.38500982522964 -0.75848639011383 -0.42694765329361 -0.98598629236221 -0.42469879984855 0.83978271484375 -0.89523947238922 0.21465709805488 -0.12998943030834 0.14889819920063 0.00240560458041 -0.75320565700531 0.15933430194854 0.84670227766037 0.49852964282035 -0.46512472629547 -0.24295699596405 -0.18003137409687 -0.248728454113 -0.44872692227363 -0.68750166893005 0.84836089611053 -0.49515345692634 -0.71375703811645 0.33617293834686 -0.58055818080902 -0.82209664583206 -0.25755333900451 0.31582978367805 -0.0927395671606 0.46614015102386 0.06124122068285 -0.53235149383544 -0.96627259254455 0.16540592908859 0.06904108822345 -0.93281900882721 0.63847684860229 -0.05675909668207 0.69842767715454 -0.96039575338363 -0.87305974960327 0.97444224357605 0.18801675736904 -0.33934590220451 -0.0012511643581 -0.20568051934242 -0.4608829319477 -0.81964272260665 0.60453200340271 0.68994504213333 -0.65562653541565 -0.56693822145462 0.45641887187957 0.94205439090728 0.34160876274108 -0.42105090618133 0.68120157718658 0.8642703294754 0.11898732185363 0.65002489089965 -0.43727365136146 -0.8059714436531 -0.69843780994415 0.38163256645202 0.75681847333908 0.42400258779525 0.9858745932579 0.42196735739708 -0.84087663888931 0.89420926570892 -0.21792398393154 0.12582926452159 0
你可以控制的一个参数是你想用梯度扫描的方向数量。例如，你可以扫描获取64或128张图像，每张图像的扩散梯度从一个稍微不同的方向应用。更多的方向导致了更高的角度分辨率（angular resolution），这使你可以对扩散的方向做出更精细的空间区分。与任何提高分辨率的东西一样，其代价是更多的扫描需要更多的时间。
5.张量建模
这种bvals和bvecs的组合使我们能够构建一个称为张量（Tensor）的东西，并将其与扩散加权图像的每个体素相匹配。在本教程中，可以把张量看作是沿x、y和z维度推动的力的模型。例如，流经花园水管的水会对管子的边界产生推力，但主要是沿着水管的长度流动。我们把能量的方向称为eigenvectors，特征向量和能量的大小称为eigenvalues,特征值。
应用于扩散加权图像，我们使用这些相同的概念，将每个体素观察到的信号建模为特征向量和特征值的组合。特征向量表示扩散的方向，而特征值代表扩散的大小。再举花园水管的例子，水的力量沿着管子的长度会有很高的特征向量和特征值；同样，我们可以把大脑中每个体素的扩散建模为特征向量和特征值的组合。一旦我们计算出最能代表当前体素中观察到的信号的数值组合，我们就可以使用一些不同的方程来计算该体素处的扩散的不同属性。这种弥散张量成像的最流行的方程式被称为分数各向异性（FA，Fractional Anisotropy），或简称为FA。这可以用公式来计算：
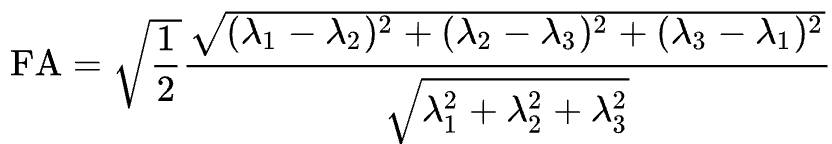各向异性是每个体素的特征值的加权和。FA值越高，说明沿某一方向的扩散越大，FA值越低，说明扩散很少，或者扩散不受约束，随意向各个方向扩散（比如说，在脑室）。如果我们发现沿其中一个维度的扩散较大，我们可以根据方向进行颜色编码。**扩散成像的惯例是用红色表示沿X轴的扩散，绿色表示沿Y轴的扩散，蓝色表示沿Z轴的扩散。**下面的图片总结了这个颜色编码方案。
在每个体素上拟合一个张量，可以生成不同类型的扩散图，如各向异性图。Tract-Based Spatial Statistics (TBSS)是一个流行的FSL扩散分析软件包，可用于创建这些地图；类似于fMRI数据的分析，这些地图可被组合成一个组分析地图，并可从地图中的感兴趣区域提取数据。
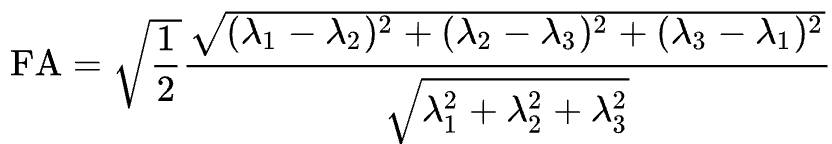FSL的TBSS生成的张量。有关如何使用此包分析主题的概述.
6.其他的扩散衡量指标
虽然FA是最流行的扩散衡量指标，但我们将简要回顾一下其他一些衡量指标：
- 平均扩散率 (Mean Diffusivity,MD)：特征值的平均值，通过将特征值相加并除以3来计算。可用于识别大脑病变，例如水肿。
- 轴向扩散系数 (Axial Diffusivity,AD)：最大特征值的值。
- 径向扩散率 (Radial Diffusivity,RD)：两个最小特征值的平均值。通常用于分析朝向相同方向的大纤维束，例如胼胝体。
7.扩散张量成像的缺点：交叉纤维问题
尽管自扩散加权成像开始以来，扩散张量成像一直是最受欢迎的分析方法之一，但它一直受到交叉纤维问题的阻碍。上述张量拟合方法对分析只包含单一方向的白质束的体素很有用。另一方面，如果体素含有相互交叉的纤维，该方法会导致虚假的结果。举个最极端的例子，设想我们获得了一个单一体素的弥散加权图像，这个体素包含相互成直角交叉的白质纤维。由于张量被限制在生成一个单一的解决方案，以估计其所有的特征向量和特征值，它无法单独估计每束纤维的扩散方向和幅度。相反，它将分割差异并得出结论，沿任何方向都没有扩散–换句话说，两个纤维束的扩散将相互抵消。
为了解决这个问题，人们开发了一种被称为球面反卷积（Spherical Deconvolution）的技术。球面反卷积不是试图为在每个体素测量的复杂信号找到一个单一的解决方案，而是假设扩散信号是你期望从多个单独的纤维在不同角度相互交叉的信号的平均值。因此，单根纤维被用作基础函数来解卷更复杂的信号。
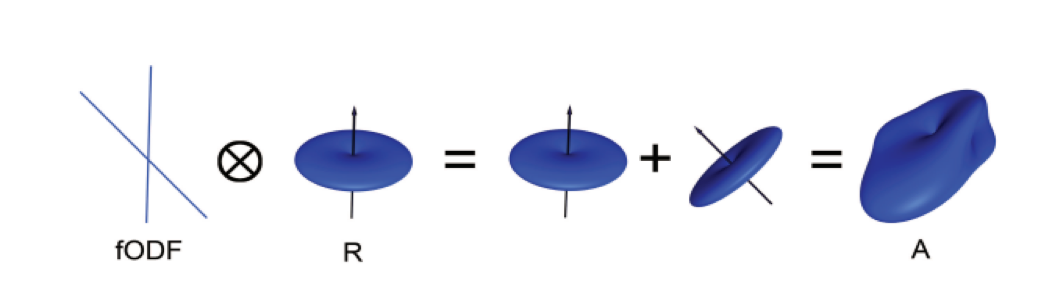
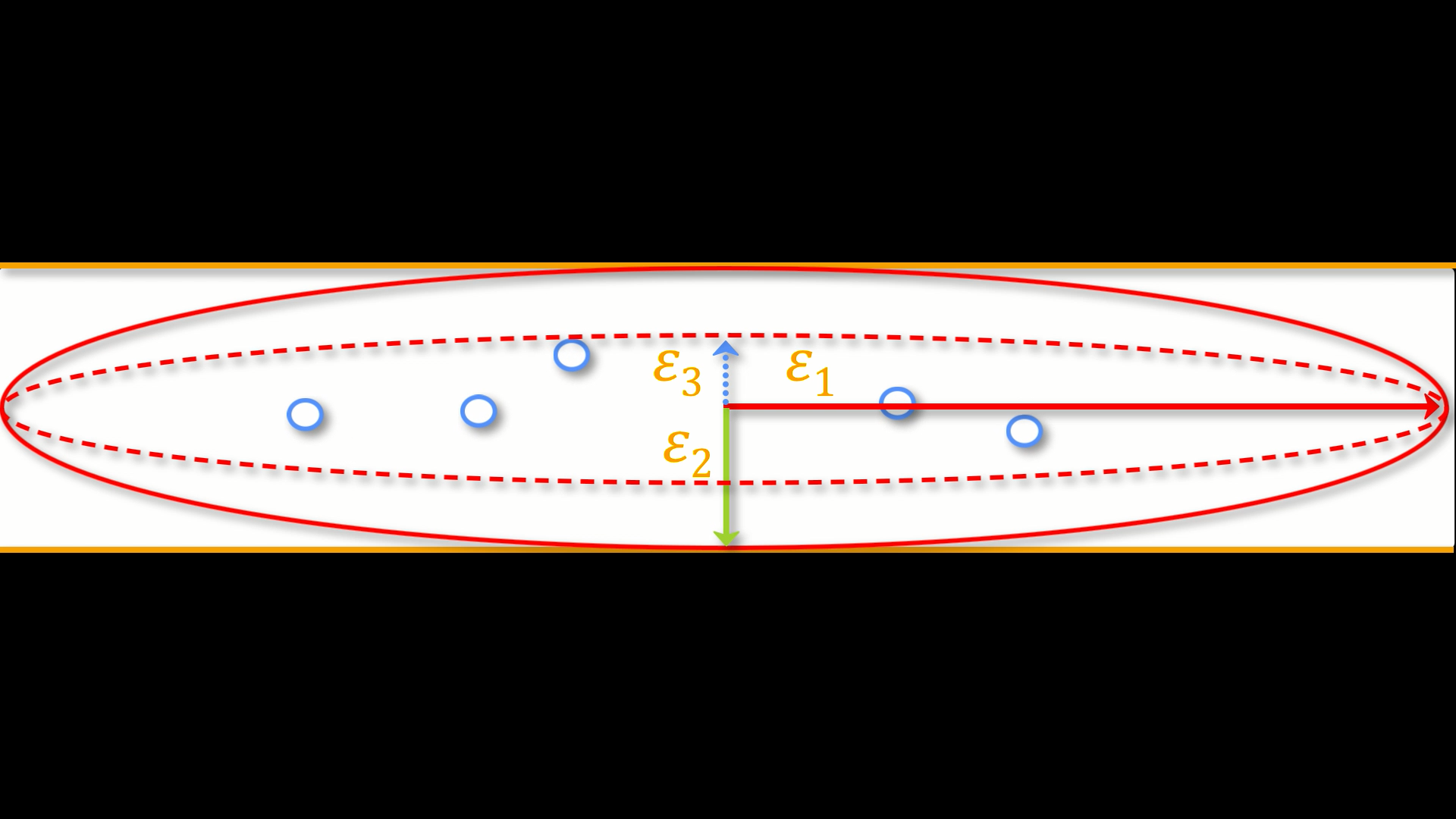
扩散加权数据从许多不同的角度获取每个体素的扩散信号，以形成扩散方向和扩散幅度的图像。然后，信号被解构为一组在不同方向上的单个纤维。球面反卷积代替了每个体素的单一扩散数，用于生成纤维取向密度函数，或FOD（Fiber Orientation Density function）。该函数被表示为一个具有卵形轴的形状；尽管加载到主要扩散方向的轴的裂片相对于其他轴变得更长、更大，但关于沿其他轴的扩散方向和强度的信息仍然被保留。
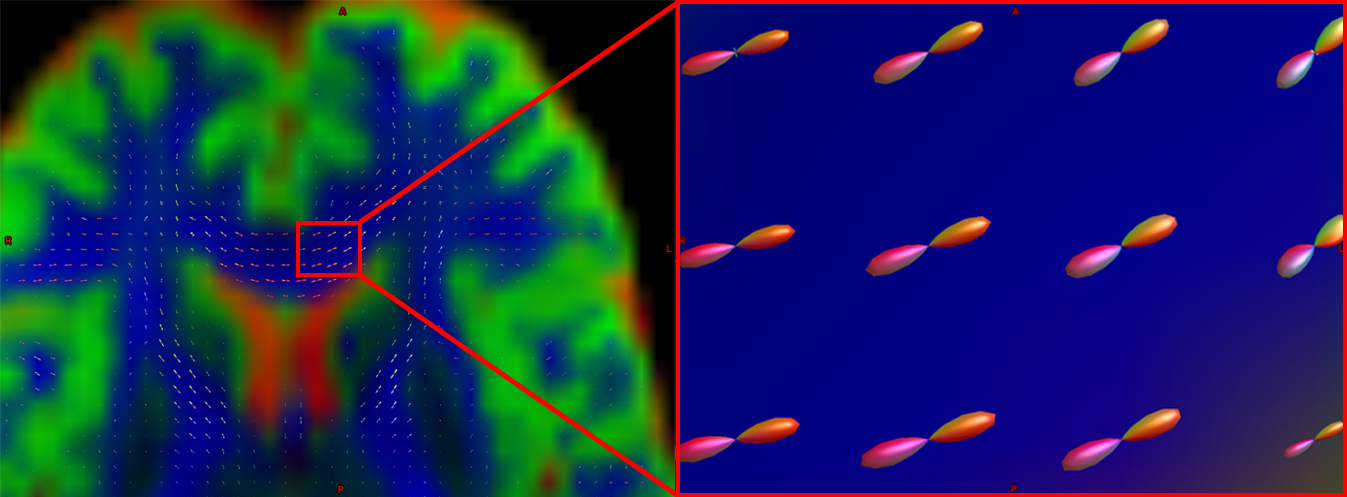
MRtrix Viewer使用
安装好mrtrix后，在终端输入命令mrview，即可打开MRtrix Viewer对扩散像数据进行可视化查看，点击UI界面上的File -> Open,选择想要查看的扩散像数据，就可以查看扩散像数据。
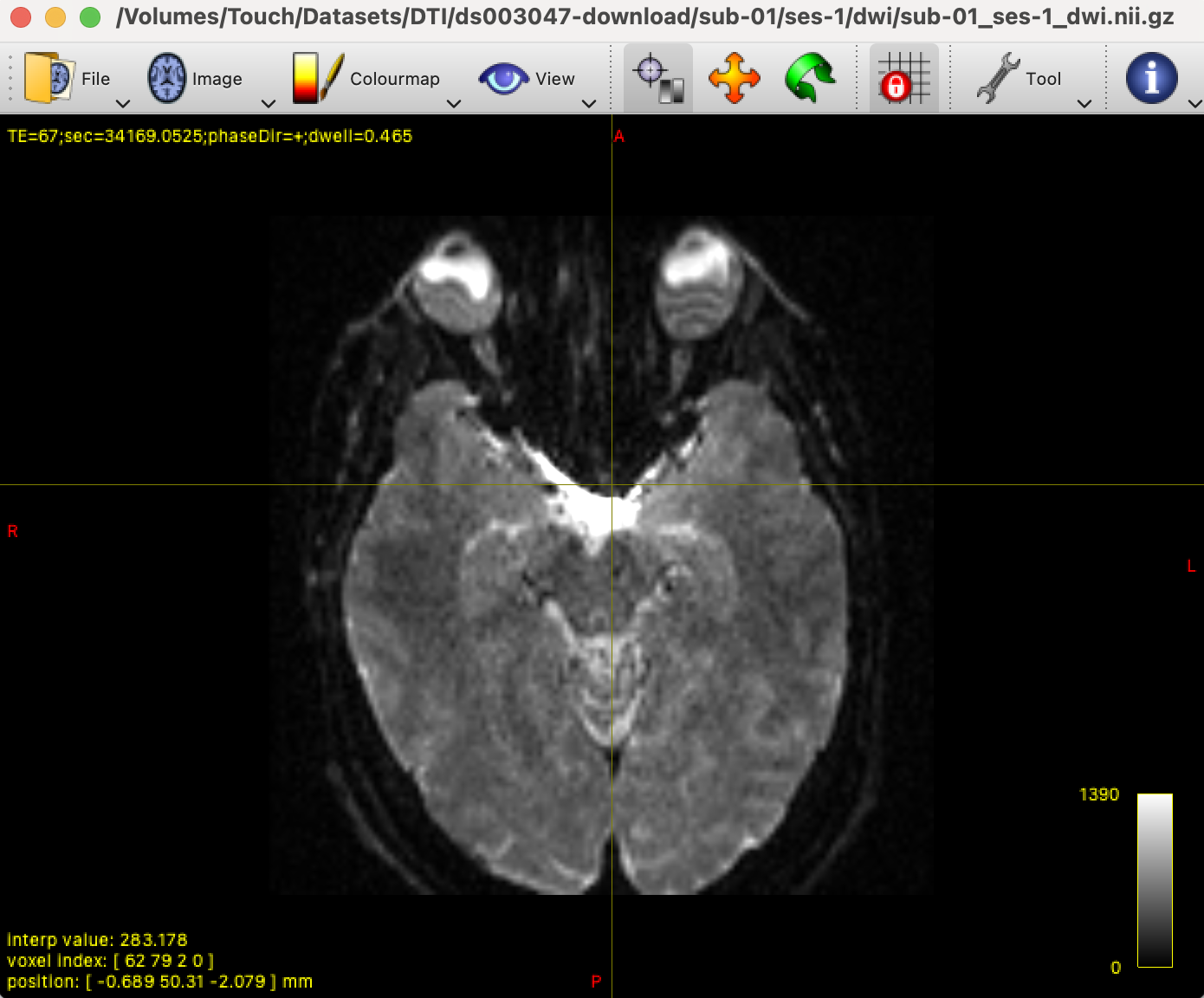
另外，我们也可以直接将文件拖拽到UI视窗，直接打开扩散像数据、结构像数据。同时，可以选择View -> Ortho view下的选项，调整为三视图模式。
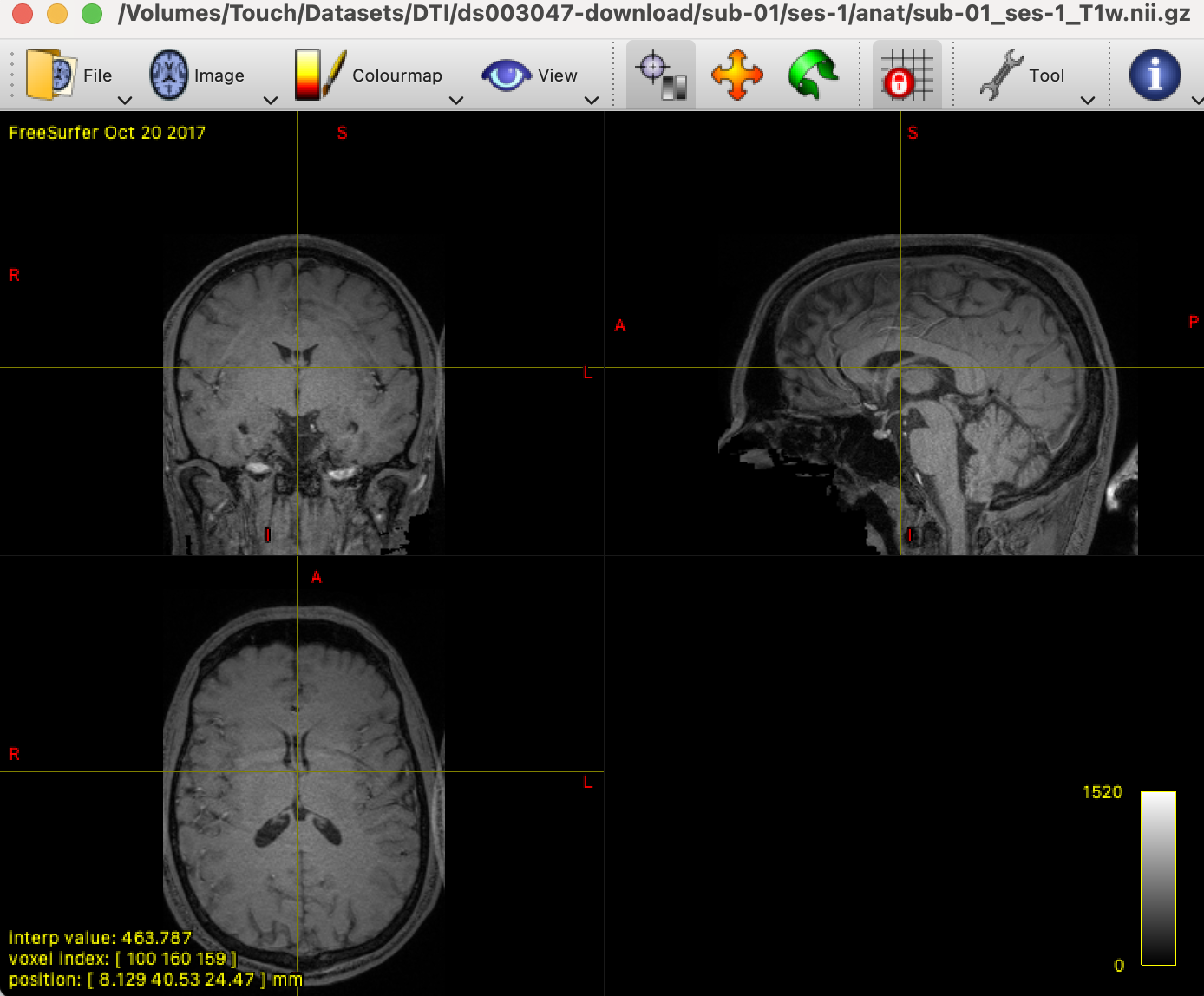
或者，使用终端方式打开一个文件查看，如下图所示：
$ mrview <*.mif>
$ mrview <*.mif> -overlay.load <*.mif>
MRtrix Viewer默认显示的第一个体积，其时间序列索引为0，即看起来像典型的 T2 加权功能图像.（0 表示时间序列中的第一个体积，1 表示第二个体积，依此类推），我们可以选择Image -> Next volume或者Image -> Go to volume跳转到不同的volume（快捷键：通过键盘左右方向键，可以快速切换volume）；视窗的左下角voxel index中最后一位，展示了当前所在的volume是哪个。
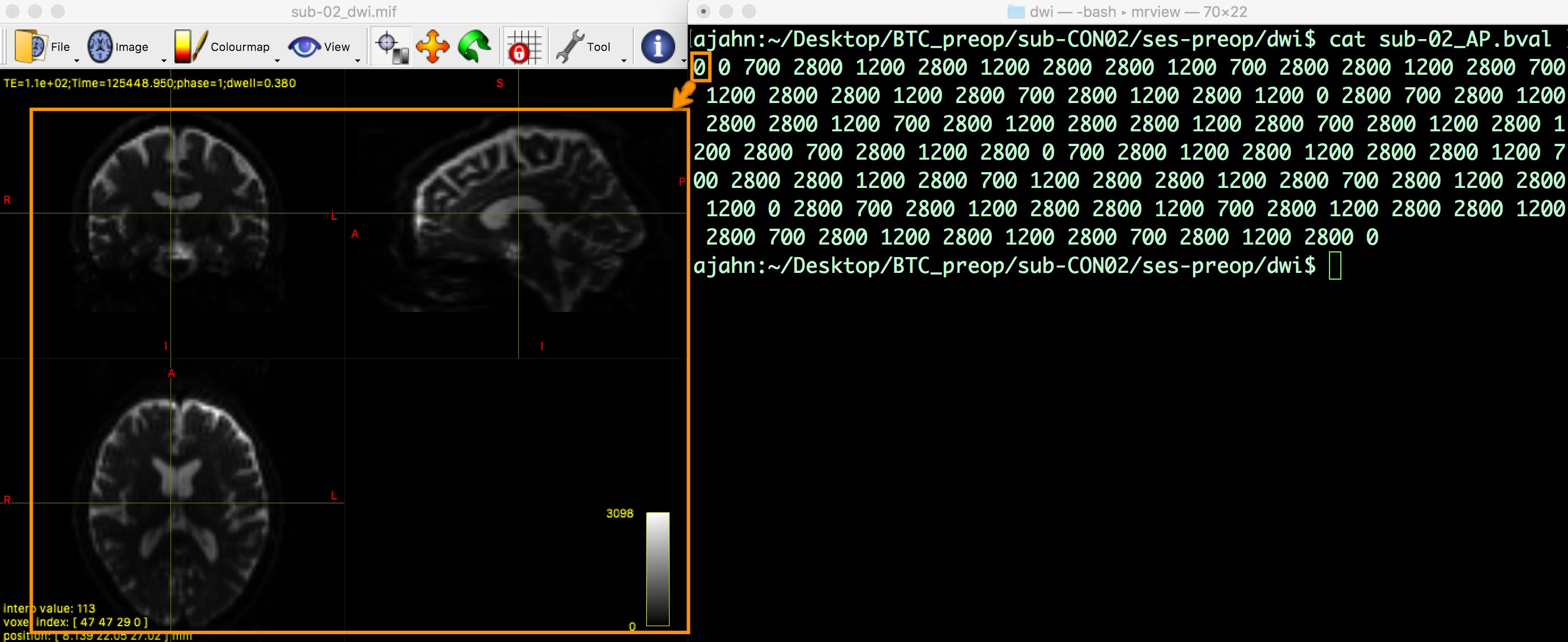
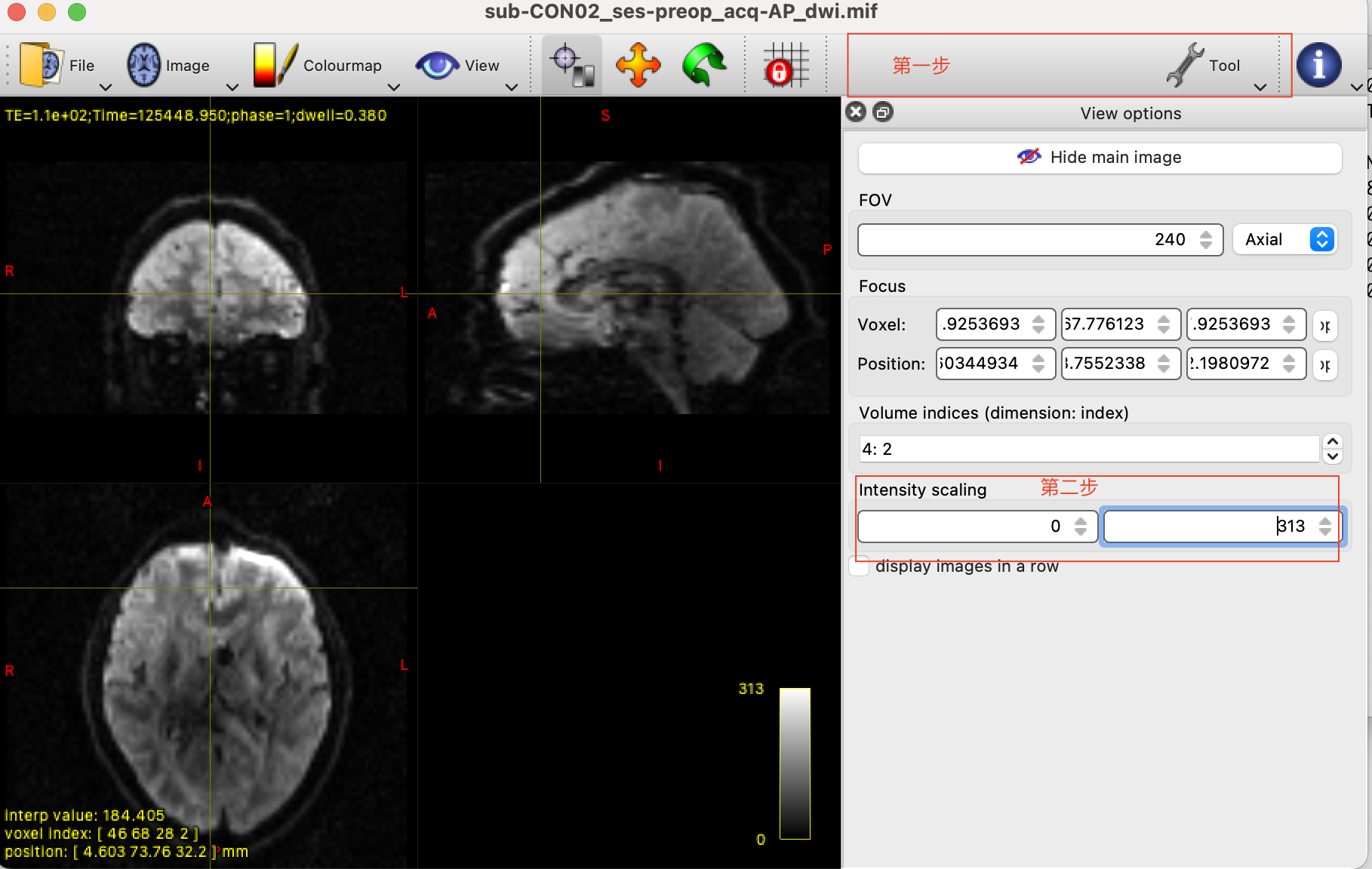
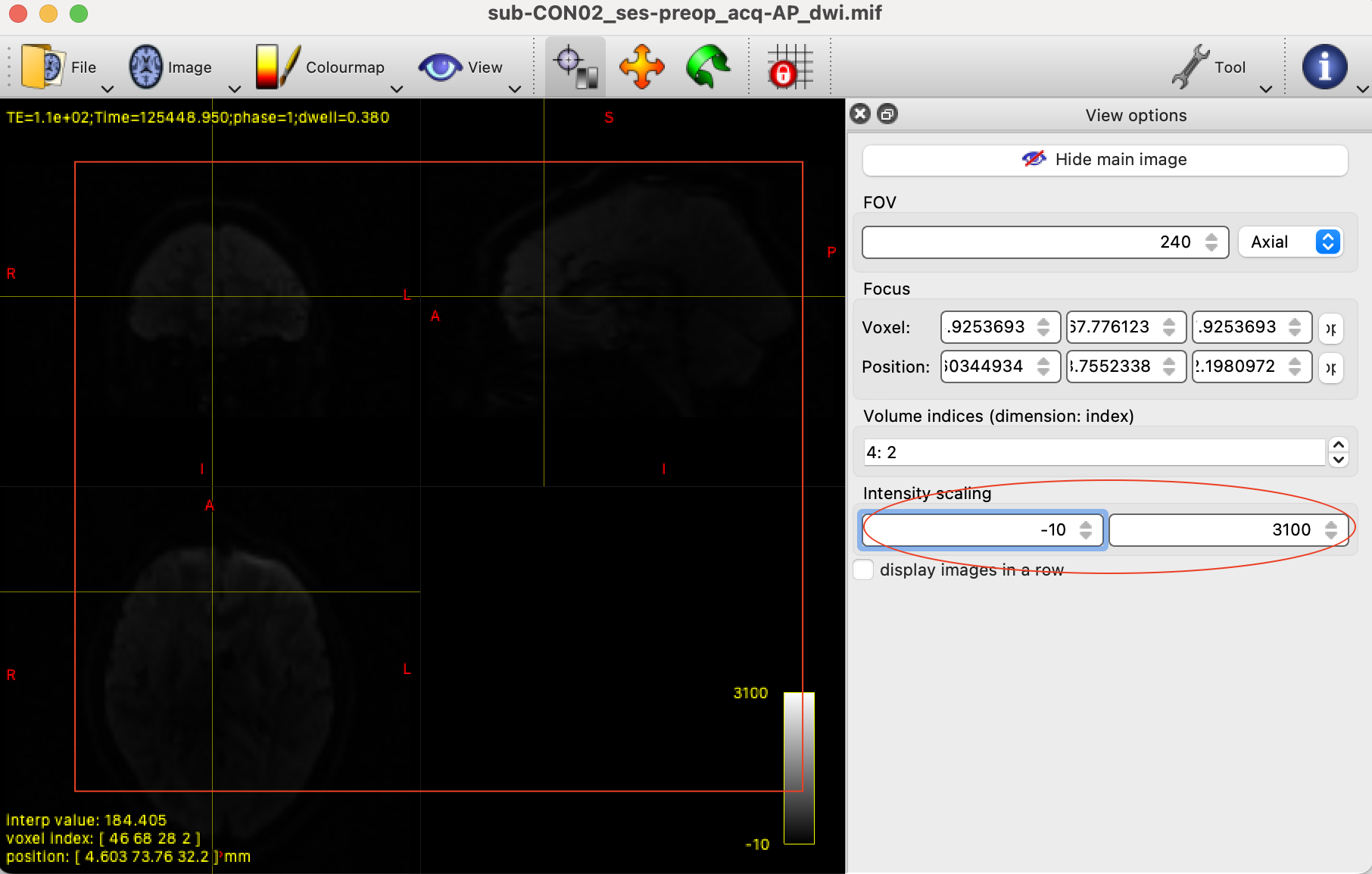如果你发现强度的下降使图像太暗而看不清，你可以通过点击Tool -> View options选项来增加亮度，然后为Intensity scaling栏输入一个较低的最大值。
BTC_preop（Brain Tumor Connectomics Data）数据下载
我们将分析来自openneuro.org的一个名为BTC preop 的数据集。
请点击前往相关网站进行数据下载。
数据集中包括11名神经胶质瘤患者、14名脑膜瘤患者和11名对照受试者的术前数据在论文"Modeling brain dynamics in brain tumor patients using The Virtual Brain"使用。
MRtrix数据格式与格式转换
MRtrix使用它自己的格式(.mif)来存储和显示成像数据。如果你已经使用过流行的fMRI软件包的教程，如SPM、FSL和AFNI，你可能记得它们都可以读取和写入NIFTI格式的图像。(AFNI默认会以它自己的BRIK/HEAD格式写文件，除非你指定你的输出应该有一个.nii扩展名，但它是唯一的例外)。MRtrix也能读取NIFTI格式的原始数据，但会以MRtrix格式输出文件，标有.mif扩展名。
要看这是如何工作的，请导航到包含dwi数据的文件夹下，其中包含你的扩散数据。预处理数据的第一步是将扩散数据转换为MRtrix能理解的格式；我们将使用mrconvert命令将原始扩散数据与相应的.bval和.bvec文件结合起来，这样我们就可以将合并的文件用于未来的预处理步骤。
# mrconvert -h 查看使用说明
# 注意mrconvert可以将mif与nii之间互相转换。
$ mrconvert -h
MRtrix 3.0.4 mrconvert Dec 14 2022
mrconvert: part of the MRtrix3 package
SYNOPSIS
Perform conversion between different file types and optionally extract a
subset of the input image
USAGE
mrconvert [ options ] input output
input the input image.
output the output image.
...
-fslgrad bvecs bvals
Provide the diffusion-weighted gradient scheme used in the acquisition in
FSL bvecs/bvals format files. If a diffusion gradient scheme is present in
the input image header, the data provided with this option will be instead
used.
...
# 将原始扩散数据与相应的`.bval`和`.bvec`文件结合起来
# mrconvert <input nifti> <output mif> -fslgrad <bvecs> <bvals>
$ mrconvert sub-CON02_ses-preop_acq-AP_dwi.nii.gz sub-CON02_ses-preop_acq-AP_dwi.mif -fslgrad sub-CON02_ses-preop_acq-AP_dwi.bvec sub-CON02_ses-preop_acq-AP_dwi.bval
# mrinfo <mif file>
# 快速查看mif数据的信息
# 输出包含例如数据集的维度和体素大小，以及用于生成当前文件的命令；
$ mrinfo sub-CON02_ses-preop_acq-AP_dwi.mif
************************************************
Image name: "sub-CON02_ses-preop_acq-AP_dwi.mif"
************************************************
Dimensions: 96 x 96 x 60 x 102
Voxel size: 2.5 x 2.5 x 2.5 x 8.7
Data strides: [ -1 2 3 4 ]
Format: MRtrix
Data type: signed 16 bit integer (little endian)
Intensity scaling: offset = 0, multiplier = 1
Transform: 0.9988 -0.01395 0.04747 -111
0.02082 0.9888 -0.1476 -85.88
-0.04488 0.1484 0.9879 -56.76
command_history: mrconvert sub-CON02_ses-preop_acq-AP_dwi.nii.gz sub-CON02_ses-preop_acq-AP_dwi.mif -fslgrad sub-CON02_ses-preop_acq-AP_dwi.bvec sub-CON02_ses-preop_acq-AP_dwi.bval (version=3.0.4)
comments: TE=1.1e+02;Time=125448.950;phase=1;dwell=0.380
dw_scheme: 0,0,0,0
[102 entries] 0,0,0,0
...
0.9082055818,0.3669468842,-0.201277434,2800
0,0,0,0
mrtrix_version: 3.0.4
请注意，由于这是一个四维数据集(96 x 96 x 60 x 102)，最后一个维度是时间；换句话说，这个文件包含102个体积(volumes)，每个体积的尺寸是96 x 96 x 60体素。体素大小(Voxel size)字段的最后一个维度值为8.7,表示获取每个体素的时间。这个时间也被称为重复时间(repetition time)，或TR。
检查Bvals和Bvecs
我们需要检查的其他文件是bvals和bvecs文件。(简而言之，bvals文件包含了每个容积的一个数字，表明应用于数据的扩散梯度有多大；bvecs文件包含了每个容积的三组数字，表明应用梯度的方向是什么。一般来说，具有较大b值的体积对扩散变化更敏感，但图像也更容易受到运动和生理伪影的影响，如下图所示。
其中，最重要的检查是确保bvals的数量和bvecs的数量与数据集中的卷数相同。
$ mrinfo -size sub-CON02_ses-preop_acq-AP_dwi.mif
96 96 60 102
# 输出mif的信息，使用awk命令，提取输出文本的第4列内容；
$ mrinfo -size sub-CON02_ses-preop_acq-AP_dwi.mif | awk '{print $4}'
102
从上述命令，我们得到mif文件中的volumes的数量为102，然后我们再来检查一下bvals和bvecs文件的数量是否一致。
$ awk '{print NF;exit}' sub-CON02_ses-preop_acq-AP_dwi.bvec
102
$ awk '{print NF}' sub-CON02_ses-preop_acq-AP_dwi.bval
102
AWK中NF用法
> $NF表示一行数据最后一列的那个值；NF表的是一行数据的列数;
> 比如有个文本内容为：
> a b c d e
> 那么awk 'print $NF'会打印出e
> awk 'print NF'会打印出5，也就是列数；
如果你的数据集中的卷数与bvals和bvecs的数量不一致，你应该向你的扫描技术员检查这个差异；文件可能没有正确上传到服务器，或者可能没有正确获得扩散加权图像。