FSL系列教程 #3. 统计与建模
简介
现在,经过预处理后,我们可以对数据进行模型拟合。为了理解模型拟合的原理,我们需要回顾一些基本原理,如一般线性模型(GLM)、BOLD反应和什么是时间序列。这些主题在下面章节中都有讨论。
在你回顾了这些概念之后,你就可以使用FEAT进行一级分析了。下图说明了我们将如何对数据进行模型拟合。
第一级分析(First Level Analysis)
1.时间序列(Time-Series)
为了理解模型拟合的工作原理,首先我们需要回顾一下fMRI数据的构成。请记住,fMRI数据集包含几个volumes,像串珠子一样串在一起–我们把这串volumes的串联称为数据run。在整个run过程中,在每个体素测量的信号被称为时间序列。
在SPM中,一个run被称为一个session。有些术语在不同的分析包中没有标准化。在本课程中将继续使用上述run的定义。
为了说明这看起来像什么,打开fsleyes浏览器,加载数据集filtered_func_data.nii.gz。在右下角有一个标记为 “Location"的窗口,有一个名为 “Volume"的字段。这表明在观察窗口中显示的时间序列的当前volume。点击该字段旁边的向上箭头,显示时间序列中的下一卷,注意从一卷到下一卷有微小但明显的变化。
要看到时间序列以更快的速度连续更新,请点击电影卷轴模样的图标"Movie Reel"。可以通过点击扳手图标(“Wrench”)来改变更新速度。
然后,点击屏幕上方的View菜单,选择时间序列(Time series)。这就打开了另一个窗口,显示整个时间序列的信号变化,X轴上是volume序号。y轴是扫描仪以任意单位来衡量采集的fMRI信号;在对每个扫描进行归一化处理后,我们可以解释这些单位,并在不同条件下比较归一化信号。

时间序列代表了在每个体素上测量的信号,但这个信号来自哪里?在下一节,我们将简要回顾fMRI的历史,以及我们如何产生你在viewer中看到的信号。
2.BOLD(血氧水平依赖,Blood Oxygen Level Dependent)信号发展历史
在整个20世纪80年代和90年代初,神经影像学研究人员将使用正电子发射断层扫描(PET)等方法测量大脑组织之间的对比度。这涉及到注射一种放射性的葡萄糖示踪剂(radioactive glucose tracer),当神经元发射时被其吸收。通过在不同的实验条件下拍摄大脑图像,如看到一个闪烁的棋盘或做一个认知要求高的问题,研究人员可以看到哪些区域与其他区域相比更活跃。
然而,这种方法是侵入性的,而且被注射放射性示踪剂的想法使许多人不敢成为这种实验的对象。到20世纪90年代初,一种被称为磁共振成像(MRI)的替代成像技术已经变得更快、更便宜,研究人员正在寻找一种方法,使其更广泛地用于临床。1990年,贝尔实验室的一位名叫Seiji Ogawa的研究人员发现,更多的脱氧血液会导致从一个大脑区域测得的信号减少。而另一方面,含氧血液的增加会增加信号–这种含氧血液的增加后来被证明与神经发射的增加相关联。这种信号的变化被称为血氧水平依赖信号(或BOLD信号)。
此后不久,在1992年,马萨诸塞州总医院(Massachusetts General Hospital)一位名叫Ken Kwong的研究人员证明,BOLD信号可被用作神经活动的间接测量。他的实验包括向受试者交替显示一个闪烁的棋盘和一个黑屏,每次一分钟。在每个条件下都记录了BOLD信号,如以下视频所示:

这个是一个重要的实验,成为许多功能神经成像实验的模板。Kwong找到了一种方法,利用体内的血液作为内源性示踪剂,对健康受试者的大脑活动进行成像,消除了对注射或辐射的需要。因此,fMRI实验变得更加流行,到2000年代初,fMRI已成为主流的神经影像学方法。
BOLD信号作为神经发射的间接测量方法 尽管Ogawa和Kwong的发现对使用MRI的神经成像者来说是一个福音,但也有一个问题:这种新方法是对大脑活动的间接测量,与实际的神经发射相差了几步。每当有刺激出现时–如闪光或突然的噪音–该刺激被感觉器官转化为神经冲动,反过来刺激大脑中的神经元发射。发射的神经元需要氧气,而氧气是由血液输送的。这种含氧的血液反过来又增加了来自附近的氢气在你体内的信号,这就是扫描仪中所测量的。
尽管如此,这也是用来推断大脑某一区域是否 “活跃 “的措施。而要做出这些推断,我们将需要仔细研究BOLD信号、实验设计,以及我们如何将两者与数学模型结合起来。
3.血流动力学反应函数(HRF,Hemodynamic Response Function)
从BOLD反应到HRF 在上一小节中,我们读到了关于BOLD信号代表什么的一些假设;我们的另一个假设是BOLD反应是什么样子。这不仅对建立神经活动和血流之间的联系、从那里到观察信号的建模很重要,而且对我们如何定义一个模型来测试哪些脑区对给定刺激的BOLD反应有明显变化也很重要。
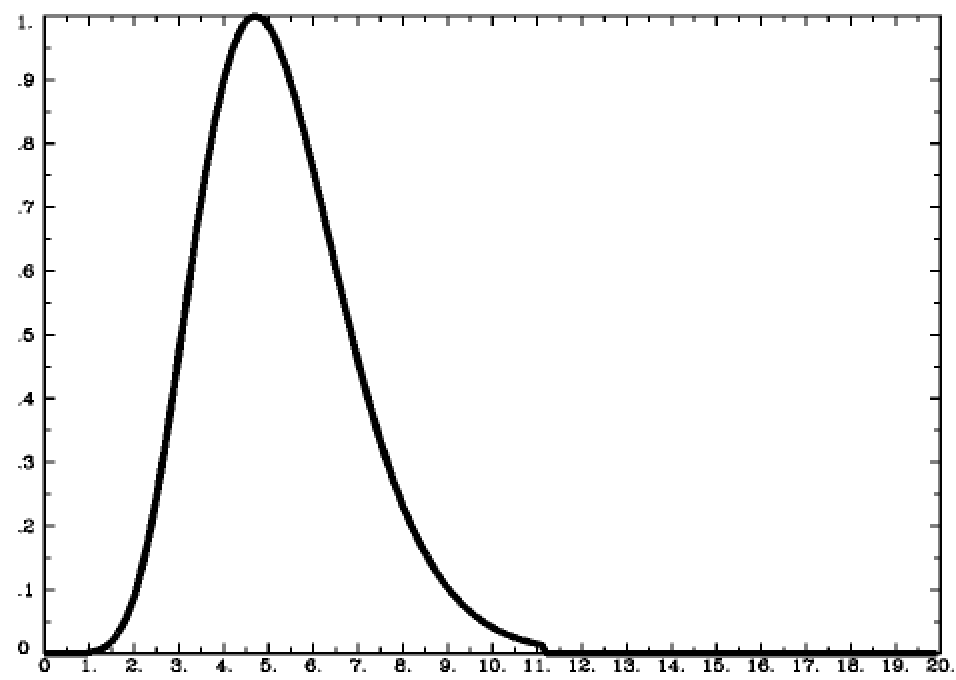
在20世纪90年代,对BOLD信号的实证研究表明,在向受试者呈现一个刺激后,大脑的任何部分对该刺激有反应–例如,视觉皮层对一个视觉刺激的反应–显示出BOLD信号的增加。BOLD信号似乎也遵循一个一致的形状,在6秒左右达到峰值,然后在接下来的几秒钟内回落到基线。这种形状可以用一个叫做伽马分布(Gamma Distribution)的数学函数来模拟。当伽马分布被创建为最适合大多数经验研究观察到的BOLD反应的参数时,我们把它称为典型的血液动力学反应函数,或HRF。
当应用于fMRI数据时,伽马分布被称为基础函数(baiss function)。我们称它为基础函数,因为它是我们将创建的模型的基本元素,或基础,并适合于数据的时间序列。此外,如果我们知道分布的形状在应对非常短暂的刺激时是什么样的,我们就可以预测它在应对不同持续时间的刺激时应该是什么样的,以及任何随时间呈现的刺激组合。现在我们来看看每种情况的说明。
单一脉冲刺激的HRF
如果一个刺激的持续时间很短,如弹指一挥间,我们可以说它是一个脉冲刺激–换句话说,它没有持续时间。正如你在下图中看到的,BOLD信号的形状看起来像一个典型的伽马分布,其峰值接近时间轴的起点(即X轴),并有一个长尾巴向右。
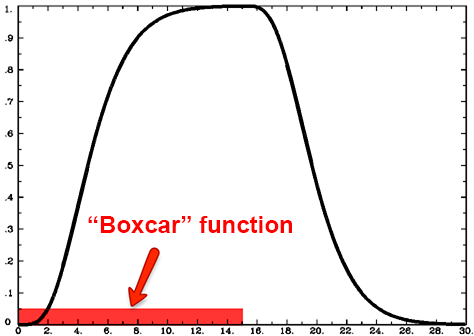
单个矩形刺激(boxcar stimulus)的HRF 尽管许多研究使用的刺激物只持续一秒钟或更短,但有些研究提出的刺激物持续时间更长。例如,想象一下,受试者看一个闪烁的棋盘15秒的时间。在这种情况下,HRF的形状将更加分散,其持续的峰值与刺激的持续时间成正比,只有在刺激结束后才回落到基线。这种刺激被称为矩形刺激(boxcar stimulus),因为它看起来像火车上的箱车的形状。
在这种情况下,伽马分布与矩形刺激进行卷积。卷积是两个函数在时间上的平均化;因此,当Gamma分布与矩形刺激平均化时,它就会扩大,而当刺激被移除时,它就会回到基线。
在单脉冲情况下,Gamma分布也是与一个刺激进行卷积的。由于脉冲刺激是无限小的,它在时间轴上被表示为一条垂直线。这就是为什么它有时被称为棒状函数(stick function)。
 )
)
如果HRFs重叠了怎么办? 我们已经看到了一个刺激呈现后的BOLD信号是什么样子,以及HRF是如何模拟该信号的形状的。但是,如果在前一个刺激的BOLD反应恢复到基线之前,又出现了另一个刺激,会发生什么?
在这种情况下,各个HRFs被加在一起。这就产生了一个BOLD反应,它是单个HRFs的移动平均值,当更多的刺激接近时,BOLD信号的形状变得更加复杂。
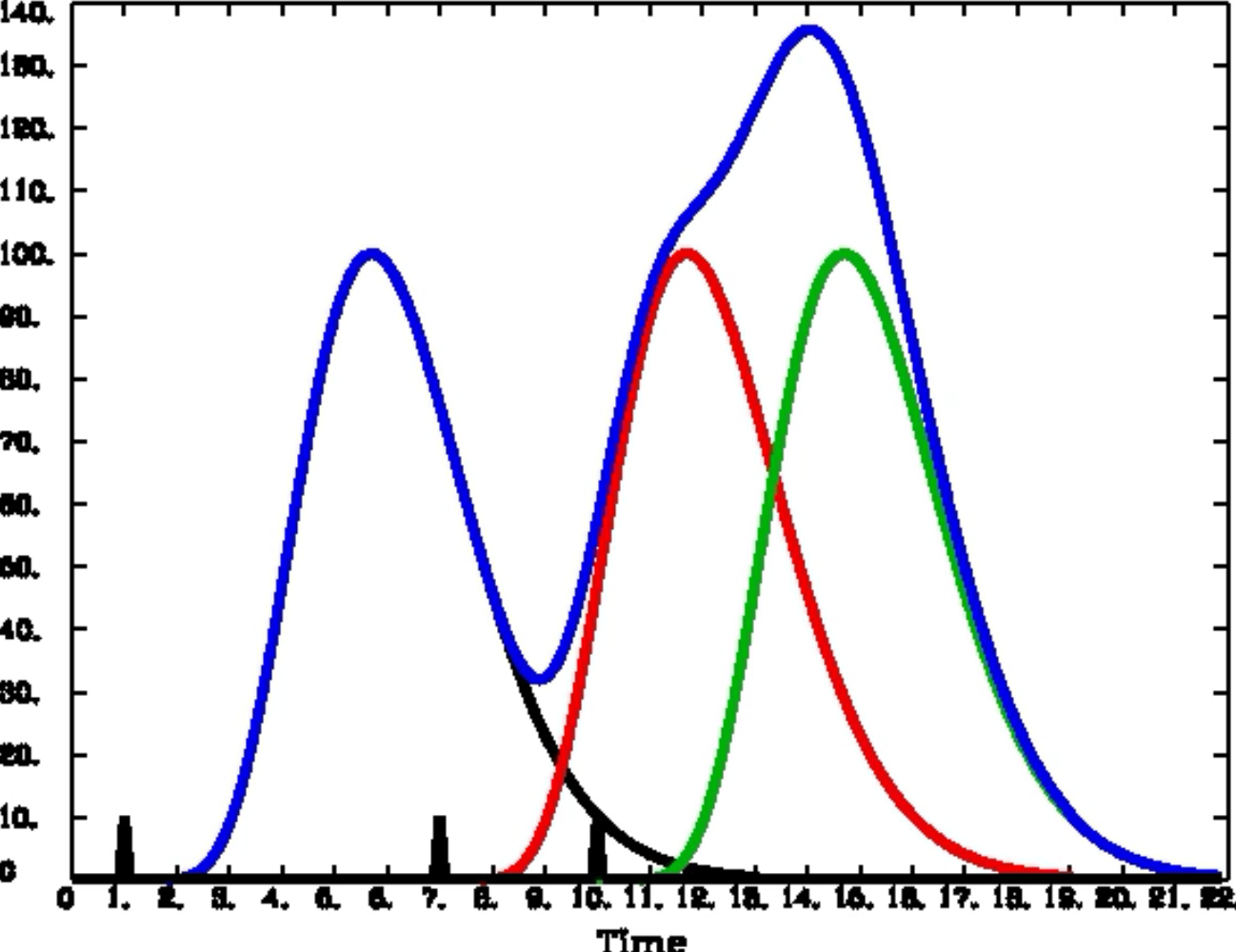
每个案例的动画 为了帮助理解刚刚阅读的内容,请多看几次下面的动画。它将显示上述每个案例是如何随着时间的推移而展开的,这将有助于我们的理解。

练习 1.在本章中,术语 “血流动力学反应函数,HRF “和 “BOLD信号 “被用来代表类似但不同的概念。你将如何用你自己的话来定义这些术语?
刚刚学到的概念可能比在本课程中以前学过的更难理解。即使觉得自己没有完全理解HRF和卷积,也要继续学习本模块的其他内容。在你读完其余章节并做完实际练习后,再来看看本章,然后看看是否有了新的理解和收获。
4.广义线性模型(General Linear Model)
本章是对广义线性模型(GLM)的简要介绍,以及如何将其应用于fMRI数据。
现在我们来看看广义线性模型,或称GLM。通过广义线性模型,我们可以使用一个或多个回归因子(regressors),或自变量(independent variables),将一个模型拟合到一些结果测量,或因变量(dependent variable)。要做到这一点,我们要计算称为β权重的数值,这是分配给每个回归因子的相对权重,用以最好的拟合数据。模型和数据之间的任何差异被称为残差(residuals)。
代表这些术语的符号显示在下面的方程式中,可以根据模型中的回归因子数量缩短或扩大。

让我们看看如何将其应用于一个简单的例子。想象一下,我们想根据身高(Height)、智商(IQ)和每周喝酒的次数(Drinks per week)来预测GPA。我们可能会发现,智商与GPA有正相关,饮酒次数有负相关,而身高则完全没有相关;我们给这些回归因子分配β权重以最适合数据。例如,也许每增加一个IQ点就会使GPA增加0.05,而每周每增加一杯饮料就会使GPA减少0.07。在这种情况下,我们的模型和它的β权重会是这样的(其中星号代表β权重是有统计学意义的,或者不可能仅仅因为偶然而与结果测量相关):

这个GLM可以扩展到包括更多回归因子,但无论有多少回归因子,GLM都假设数据可以被建模为回归因子的线性组合–因此被称为广义线性模型,GLM。我们将在下一节中看到如何将GLM应用于fMRI数据。
5.创建Timing Files
理想时间序列和拟合时间序列 我们刚刚看到如何使用几个回归因子,或自变量,来估计一个结果测量,如GPA。从概念上讲,当我们使用几个回归因子来估计大脑活动时,我们也在做同样的事情,大脑活动是我们用fMRI数据衡量的结果:我们估计BOLD信号的平均振幅,以响应我们模型中的每个条件。
在下面的动画中,BOLD反应的不同颜色代表不同的条件(如Congruent和Incongruent),灰线代表我们预处理数据的timecourse。这表明每个条件的振幅是如何被估计为最适合数据的;对于左边的条件,它相对较高,而对于右边的条件,它相对较低。也可以想象一个条件的BOLD信号与零没有显著差异,甚至是负数。

代表HRFs的红线和绿线被称为理想时间序列(ideal time-series)。这是我们期望的时间序列,鉴于我们实验中每个刺激的时间。当我们估计β权重来拟合这个理想时间序列的数据时,其结果被称为拟合时间序列(fitted time-series),在动画中显示为一条蓝线。
由于每个体素都有自己的时间序列,我们对大脑中的每个体素进行上述程序。这被称为大规模单变量分析,因为我们为每个体素的时间序列估计β权重。由于在一个典型的fMRI数据集中有几万或几十万个体素,以后我们需要对我们所做的所有测试进行校正。这将在后面关于组分析的一章中涉及。
创建理想的时间序列 我们的目标是创建拟合时间序列,这样我们就可以在组分析中使用估计的β权重。但是要做到这一点,我们首先需要创建我们理想时间序列。
让我们看一下Flanker数据集。在每个被试的func目录下都有标记为events.tsv的文件。这些文件包含三个信息,我们需要这些信息来创建我们的计时文件(timing files)(也称为onset files):
- 条件的名称;
- 条件的每次试验发生的时间,以秒为单位,相对于扫描的开始时间;
- 每次试验的持续时间。
这些需要从events.tsv文件中提取出来,并以FSL软件可以读取的方式进行格式整理。在这种情况下,我们将为每个条件创建一个timing文件,然后根据条件的运行情况来分割该文件。那么,我们总共将创建四个timing文件:
- 在第一次run中发生的不一致试验的计时(我们将称之为incongruent_run1.txt);
- 第二次run中出现的不一致试验的时间(incongruent_run2.txt);
- 第一次run时发生的一致性试验(Congruent trials)的时间(congruent_run1.txt);
- 在第二次run中发生的一致性试验(Congruent trials)的时间(congruent_run2.txt)。
每个计时文件都有相同的格式,由三栏组成,顺序如下:
- 开始时间,以秒为单位,相对于扫描的开始时间;
- 试验的持续时间,以秒计;
- 参量调制(Parameter modulation)。
我们将在未来的模块中讨论参数调制。现在,我们需要知道的是,这是一个必要的列,除非你有参数调制的试验(在这个Flanker数据集中没有),否则就把它设置为每个试验的值为 “1”。
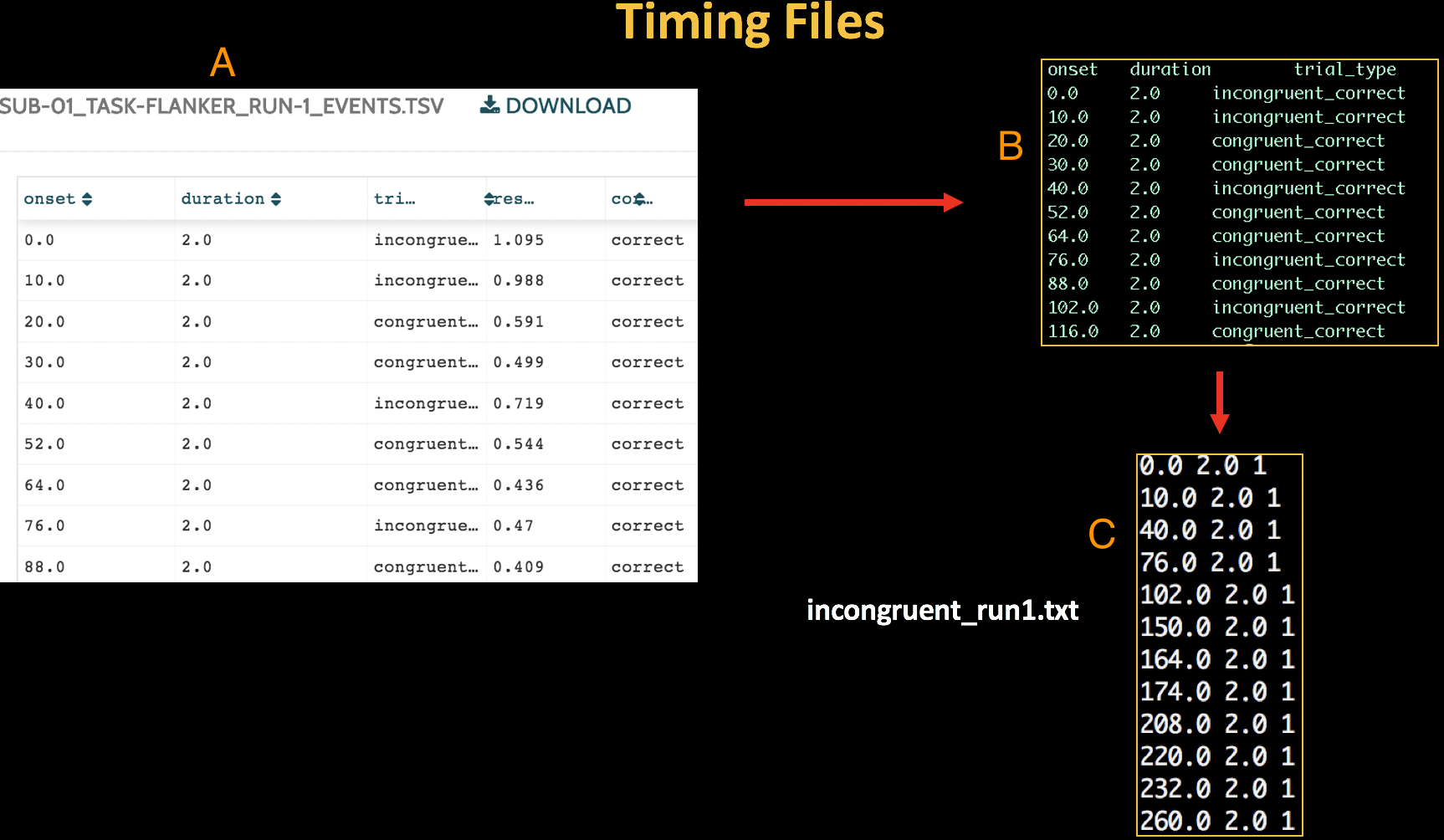
要想自动格式化计时文件,请下载这个脚本。(1. 你可以通过点击Raw按钮下载,然后在新打开的窗口中点击右键,选择 “另存为”;2. 下述有完整的该make_FSL_Timings.sh脚本,直接粘贴使用即可。)。我们不会详细介绍它是如何工作的,但你所需要做的就是把它放在包含受试者的实验文件夹里,然后输入bash make_FSL_Timings.sh。这将为每个受试者的每次运行创建计时文件。要检查输出,输入cat sub-08/func/incongruent_run1.txt。你应该看到与上图类似的数字。
| onset | duration | trial_type | response_time | correctness | StimVar | Rsponse | Stimulus | cond |
|---|---|---|---|---|---|---|---|---|
| 0 | 2 | incongruent_correct | 1.095 | correct | 2 | 1 | incongruent | cond003 |
| 10 | 2 | incongruent_correct | 0.988 | correct | 2 | 1 | incongruent | cond003 |
| 20 | 2 | congruent_correct | 0.591 | correct | 1 | 1 | congruent | cond001 |
| 30 | 2 | congruent_correct | 0.499 | correct | 1 | 1 | congruent | cond001 |
| 40 | 2 | incongruent_correct | 0.719 | correct | 2 | 1 | incongruent | cond003 |
| 52 | 2 | congruent_correct | 0.544 | correct | 1 | 1 | congruent | cond001 |
| 64 | 2 | congruent_correct | 0.436 | correct | 1 | 1 | congruent | cond001 |
| 76 | 2 | incongruent_correct | 0.47 | correct | 2 | 1 | incongruent | cond003 |
| 88 | 2 | congruent_correct | 0.409 | correct | 1 | 1 | congruent | cond001 |
| 102 | 2 | incongruent_correct | 0.563 | correct | 2 | 1 | incongruent | cond003 |
| 116 | 2 | congruent_correct | 0.493 | correct | 1 | 1 | congruent | cond001 |
| 130 | 2 | congruent_correct | 0.398 | correct | 1 | 1 | congruent | cond001 |
| 140 | 2 | congruent_correct | 0.466 | correct | 1 | 1 | congruent | cond001 |
| 150 | 2 | incongruent_correct | 0.518 | correct | 2 | 1 | incongruent | cond003 |
| 164 | 2 | incongruent_correct | 0.56 | correct | 2 | 1 | incongruent | cond003 |
| 174 | 2 | incongruent_correct | 0.533 | correct | 2 | 1 | incongruent | cond003 |
| 184 | 2 | congruent_correct | 0.439 | correct | 1 | 1 | congruent | cond001 |
| 196 | 2 | congruent_correct | 0.458 | correct | 1 | 1 | congruent | cond001 |
| 208 | 2 | incongruent_correct | 0.734 | correct | 2 | 1 | incongruent | cond003 |
| 220 | 2 | incongruent_correct | 0.479 | correct | 2 | 1 | incongruent | cond003 |
| 232 | 2 | incongruent_correct | 0.538 | correct | 2 | 1 | incongruent | cond003 |
| 246 | 2 | congruent_correct | 0.54 | correct | 1 | 1 | congruent | cond001 |
| 260 | 2 | incongruent_correct | 0.622 | correct | 2 | 1 | incongruent | cond003 |
| 274 | 2 | congruent_correct | 0.488 | correct | 1 | 1 | congruent | cond001 |
0 2 1
10 2 1
10 2 1
40 2 1
76 2 1
150 2 1
164 2 1
174 2 1
208 2 1
220 2 1
232 2 1
260 2 1
#!/bin/bash
#Check whether the file subjList.txt exists; if not, create it
if [ ! -f subjList.txt ]; then
ls -d sub-?? > subjList.txt
fi
#Loop over all subjects and format timing files into FSL format
for subj in `cat subjList.txt` ; do
cd $subj/func #Navigate to the subject's func directory, which contains the timing files
#Extract the onset times for the incongruent and congruent trials for each run. NOTE: This script only extracts the trials in which the subject made a correct response. Accuracy is nearly 100% for all subjects, but as an exercise the student can modify this to extract the incorrect trials as well.
cat ${subj}_task-flanker_run-1_events.tsv | awk '{if ($3=="incongruent_correct") {print $1, $2, "1"}}' > incongruent_run1.txt
cat ${subj}_task-flanker_run-1_events.tsv | awk '{if ($3=="congruent_correct") {print $1, $2, "1"}}' > congruent_run1.txt
cat ${subj}_task-flanker_run-2_events.tsv | awk '{if ($3=="incongruent_correct") {print $1, $2, "1"}}' > incongruent_run2.txt
cat ${subj}_task-flanker_run-2_events.tsv | awk '{if ($3=="congruent_correct") {print $1, $2, "1"}}' > congruent_run2.txt
cd ../..
done
上述脚本是匹配生成所有被试的timing files,当然我们可以选择一个指定的events.tsv文件来生成,主要还是借鉴上述代码,其中$3表示第3列(trial_type),如果匹配上了对应的关键词,比如"incongruent_correct",那么我们就输出其$1和$2,即分别为第1列(onset)和第2列(duration):
# cat <your_events.tsv> |awk '{if ($3=="incongruent_correct"){print $1,$2,"1"}}'
$ cat sub-01_task-flanker_run-1_events.tsv |awk '{if ($3=="incongruent_correct"){print $1,$2,"1"}}'
0.0 2.0 1
10.0 2.0 1
40.0 2.0 1
76.0 2.0 1
102.0 2.0 1
150.0 2.0 1
164.0 2.0 1
174.0 2.0 1
208.0 2.0 1
220.0 2.0 1
232.0 2.0 1
260.0 2.0 1
一旦我们创建了计时文件,我们就可以用它们来为fMRI数据拟合一个模型。
6.第一级分析(First-Level Analysis)操作实践
统计数据标签,Stats
导航到sub-08目录,在命令行中输入fsl。打开FEAT图形用户界面,在数据标签右上方的下拉菜单中,将 “Full Analysis"改为 “Statistics”。这将使"Pre-stats"和"Registration"标签变灰。我们还会看到一个新的按钮,叫做 “Input is a FEAT directory”。点击该按钮,并选择你在上一模块中创建的FEAT目录run1.feat。点击确定,忽略关于从design.fsf文件加载设计信息的警告。(因为我们还没有建立模型,所以没有什么会被覆盖。)
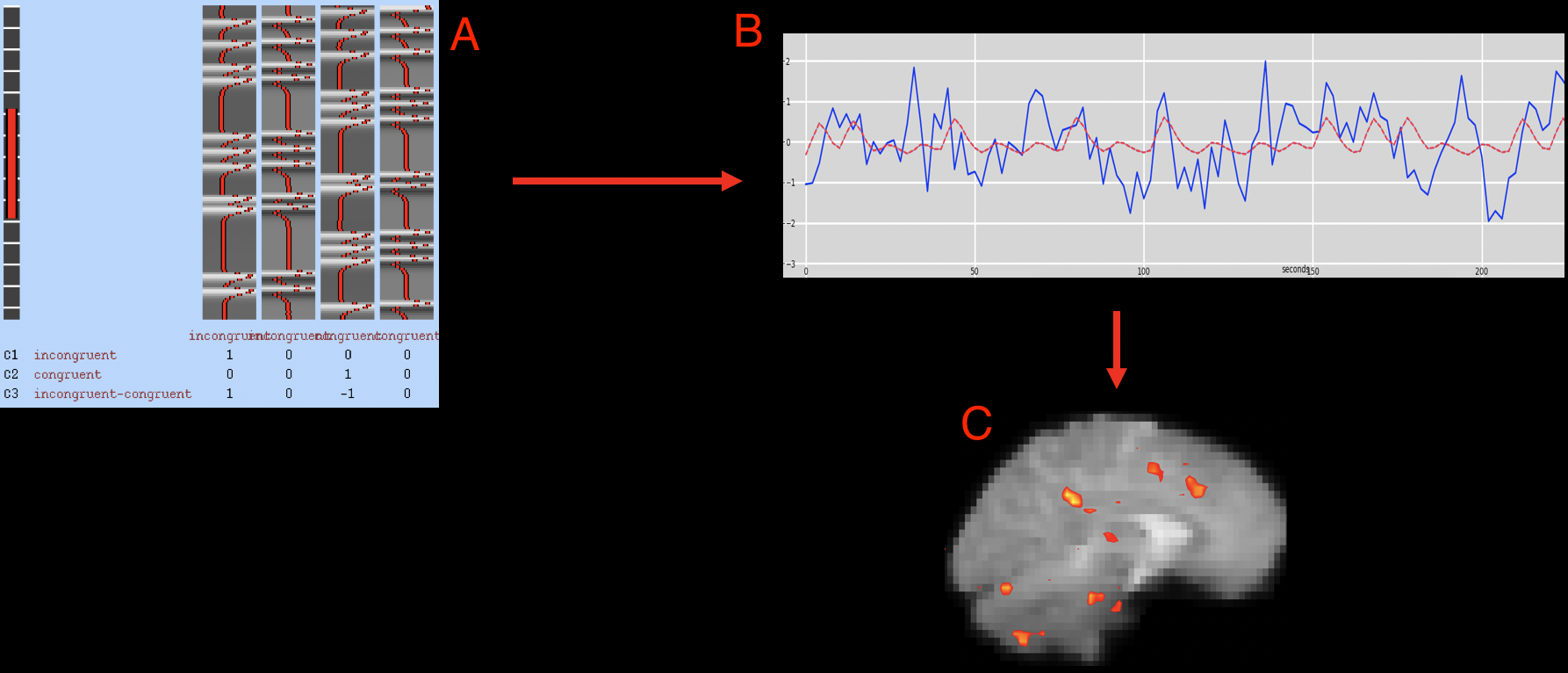
接下来,点击 “Stats"选项卡。有许多选项,但我们将只关注其中的几个。点击 “Full model setup”,并将原始EV(Original EVs,或解释变量(Explanatory Variables),FSL对回归因子的称呼)的数量改为2。在回归因子1的EV名称栏中,输入 “incongruent”。点击基本形状旁边的下拉菜单,选择 “Custom (3 column format)"。这显示了一个名为"Filename"的字段;点击文件夹图标,选择时间文件incongruent_run1.txt。取消对 “Add temporal derivate"按钮的勾选。(这是为了让我们更容易理解设计矩阵;我们将在后面添加导数)。点击 “2 “标签,重复这些步骤,这次选择计时文件congruent_run1.txt。
当我们完成了模型的设置,点击Contrasts & F-tests标签。在这里,可以指定在每个条件的β权重被估计后,你想创建哪些对比图(contrast maps)。在这个实验中,我们对三个对比感兴趣:
- 与基线相比,不一致(incongruent)条件的平均β权重;
- 与基线相比,一致(congruent)条件的平均β权重;
- 不一致条件和一致条件之间的平均β权重的差异。
设置对比度的数量为3,并在每一行输入以下对比度名称,同时在EV1和EV2列输入以下对比度权重:
- incongruent [1 0];
- congruent [0 1];
- incongruent-congruent [1 -1]。
在FSL中,β权重被称为参数估计值(parameter estimates),或称pe’s,而β权重之间的对比被称为参数估计值的对比(contrast of parameter estimates),或称cope’s。当我们检查输出数据时,你会看到两个参数估计文件(每个条件一个),以及三个参数估计对比文件(每个对比一个)。上面的对比号1和2将与参数估计文件相同;然后重新创建它们似乎是多余的,但我们将看到,FSL将要求这些文件被标记为cope’s,以便进行更高级别的分析(higher-level analysis)。
点击 “Done"按钮,将打开一个设计矩阵窗口。最左边的一列代表高通滤波器,它去除任何长于红条长度的频率(也就是说,低频被去除,而高频被允许通过滤波器)。右边的两列代表两个回归因子的理想时间序列,它们与我们输入时间文件的顺序相对应;换句话说,第一列是incongruent条件的理想时间序列,第二列是congruent条件的理想时间序列。
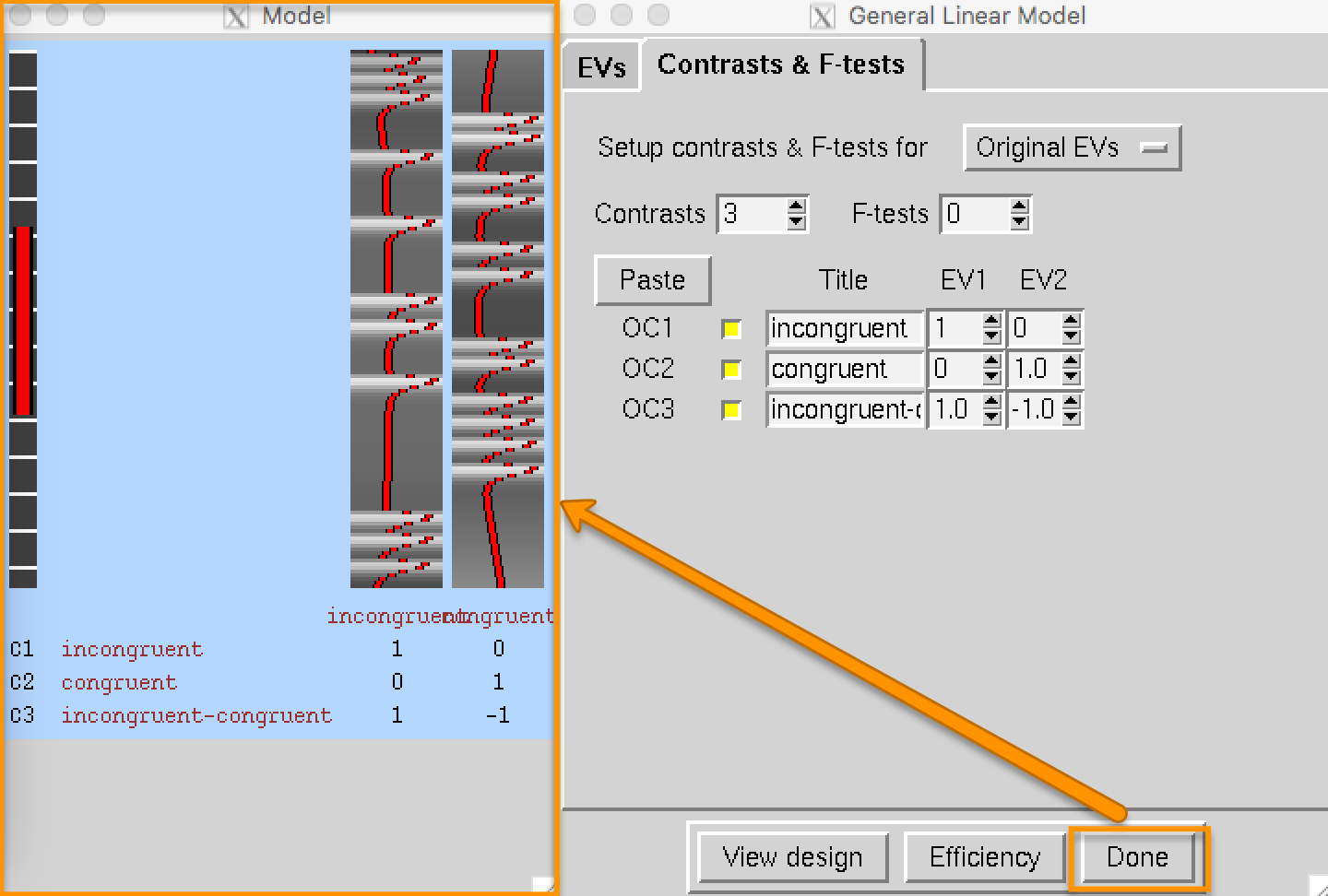
红线代表我们认为如果体素对该回归因子有反应,它的时间序列应该是什么样子。我们会注意到,白条代表的是与该条件下每次试验的开始时间相卷积的HRF。再看一下每个条件的时间文件,看看onset时间和设计矩阵之间的对应关系对你来说是否有意义。然后,点击 “Go"来运行模型。

后期统计标签,Post-Stats
FEAT图形用户界面的最后一个选项卡叫做Post-stats。同样,这里有很多选项,而唯一可能改变的是标有 “Z threshold “和 “Cluster P threshold"的选项,这些阈值决定了哪些体素对每个对比度具有统计学意义。我们现在先不考虑这些,等做组分析时再来考虑这些选项。
理想的时间序列和GLM 在点击 “Go"之后,一系列的HTML页面将被打开,以跟踪模型拟合的进展,这将需要5-10分钟才能完成。在等待的时候,让我们看看刚刚创建的模型与GLM的关系。记住,每个体素都有一个BOLD时间序列(我们的结果测量),我们用Y表示。这些回归因子构成我们的设计矩阵,我们用一个大的X来表示。
到目前为止,所有这些变量都是已知的–Y是从数据中测得的,而x1和x2是通过对HRF和时间起始点(time onsets)进行卷积而成的。由于矩阵代数是用来设置设计矩阵和估计β权重的,所以方向要转九十度: 通常我们认为时间轴是由左至右,但它被描述为由上至下。换句话说,运行的开始是在时间轴的顶部。
GLM方程的下一部分是β权重,我们用B1和B2表示。这些代表了我们对HRF需要对每个回归因子进行缩放以最好地匹配Y中的原始数据的估计,因此被称为 “β权重”。这个方程的最后一项是E,代表残差,或者说我们的理想时间序列模型和估计β权重后的数据之间的差异。如果模型拟合得好,残差就会减少,而且一个或多个β权重更有可能具有统计学意义。下面的动画显示了GLM与你创建的fMRI模型的对应关系。

检查输出 当模型估计完成后,点击 “Stats"链接,查看设计矩阵。这与我们刚才审查的结果相同;下面还有一个标有 “Covariance matrix"的图。现在,要知道,如果检测每个对比度所需的信号变化百分比低于2%,那就是合理的。
点击"Post-stats"链接可以看到每个对比度的阈值图(threshold map)。这显示了每个对比图中通过FEAT GUI的"Post-stats"标签中指定的显著性阈值的任何体素。
理解模型拟合(model fitting)和第一级分析(first-level analysis)可能具有挑战性。如果在第一次阅读这些章节时没有理解所有的内容,也不要气馁;坚持下去,随着时间和实践的推移,这些概念会变得更加清晰。
第二级分析,2nd-Level Analysis
学习前提:在学习本小节和下一小节内容时,建议提前先看fsl的脚本编写教程,便于提前准备好已预处理完的数据。
一旦对Flanker数据集中的所有受试者的运行进行了预处理和分析,我们就可以运行第二级分析了。AFNI和SPM将第二级分析定义为组分析的同义词,而在FSL中,第二级分析是将每个受试者的参数估计和第一级分析的对比估计平均化。
在Flanker目录下,通过输入Feat_gui从命令行打开FEAT GUI。然后从下拉菜单中选择Higher-Level Analysis。这就把输入栏改为Select FEAT directories。
Data标签上的下拉菜单允许你选择输入是Inputs are lower-level FEAT directories(默认),或者Inputs are 3D cope images from FEAT directories。选择FEAT目录可以让你选择分析哪些cope图像,尽管如果你没有用FSL的默认处理流来分析数据(即数据没有组织在FEAT目录中),直接选择cope图像可以给你更多的灵活性。
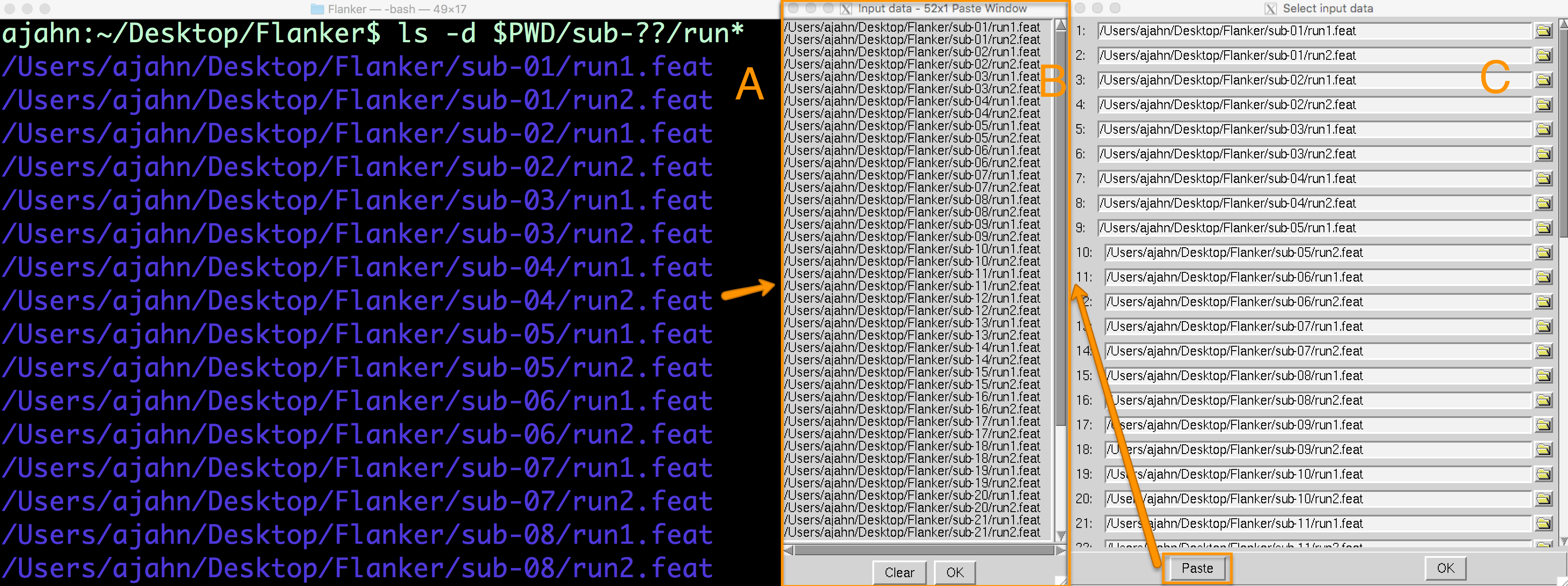
选择FEAT目录 由于我们有26个受试者,每个受试者有2次run,我们总共有52个FEAT目录。将输入的数量改为52,然后点击选择FEAT目录的按钮。
我们可以用手选择每一个FEAT目录,点击文件夹图标,逐个选择。但正如我们在编写分析脚本时看到的那样,这通常不是一个好主意–对于大型数据集来说,这是不现实的,而且犯错误的几率会随着受试者数量的增加而增加。
相反,我们将使用通配符来使其更快更容易。回到你启动FEAT图形用户界面的终端,导航到Flanker目录,输入ctrl+z,然后输入bg并按回车键。这将允许你在终端中输入命令,同时保持FEAT GUI的运行。在命令行中,输入以下内容:
ls -d $PWD/sub-??/run*
这将打印出每个FEAT目录的绝对路径。选项-d意味着只列出目录,而$PWD则扩展为指向当前工作目录的绝对路径。在当前目录中,任何以子开头、以两位数结尾的目录(用?的通配符表示)都被添加到路径中。最后,在每个被试目录内,任何以字符串run开头的目录都将被附加到路径名中(例如,run1.feat和run2.feat)。
这将创建一个有52个条目的列表,其中一个对应于研究中每个被试的每个run。突出显示整个列表,并按command+c复制它。这将把列表复制到您的剪贴板上。然后回到 “Select input data"窗口,点击 “Paste"按钮。在输入数据窗口中点击,然后按ctrl+y并点击确定。这将把目录列表粘贴到 “Select input data"窗口的相应行中。
在Data选项卡中,你会看到现在有3个较低级别的cope,你可以选择进行分析。如果你把这三个框都选上,它将为每个框运行一个第2级分析,这对应于:
1.不一致条件下的对比估计值; 2.一致条件下的对比度估计值; 3.不一致条件下的对比度估计值减去一致条件下的对比度估计值(即取参数估计值的差)。
在Output directory中,输入Flanker_2ndLevel。这就是第二层分析结果的保存位置。
创建GLM
Stats选项卡的外观将与用于第一级分析时不同–现在可以选择不同的推理类型,或者希望结果如何归纳到人群中。下拉菜单有以下选项:
Fixed Effects: 不从样本中归纳–只取平均值; Mixed Effects: Simple OLS (Ordinary Least Squares)): 简单OLS(普通最小二乘法): 这将对为每个受试者计算的平均参数估计值进行t检验,而不考虑每个受试者的运行之间的差异性; Mixed Effects: FLAME 1):通过对比估计的方差对每个受试者的参数估计进行加权。换句话说,方差相对较小的受试者将被加权,而方差相对较大的受试者将被减权; Mixed Effects:FLAME 1+2): FLAME 1的一个更严格的版本。它需要更长的时间,而且只对分析小样本(例如,10个或更少的受试者)有帮助; Randomise:一种非参数检验(在后面的章节中讨论)。
由于我们只是想在每个受试者中取得各次运行的参数估计值的平均值,我们将使用Fixed Effects选项。一旦你选择了这个选项,点击Full Model Setup。
这将显示一个窗口,其行数代表单个参数估计值的数量–在我们的例子中是52。对于Number of main EVs,将其改为26,这是我们数据集中的受试者数量。然后将每一列中的数字改为1,在这里你要对该被试的参数估计值取平均值。在我们的例子中,第1列的前两行将被改为1,第2列的后两行将被改为1,以此类推。
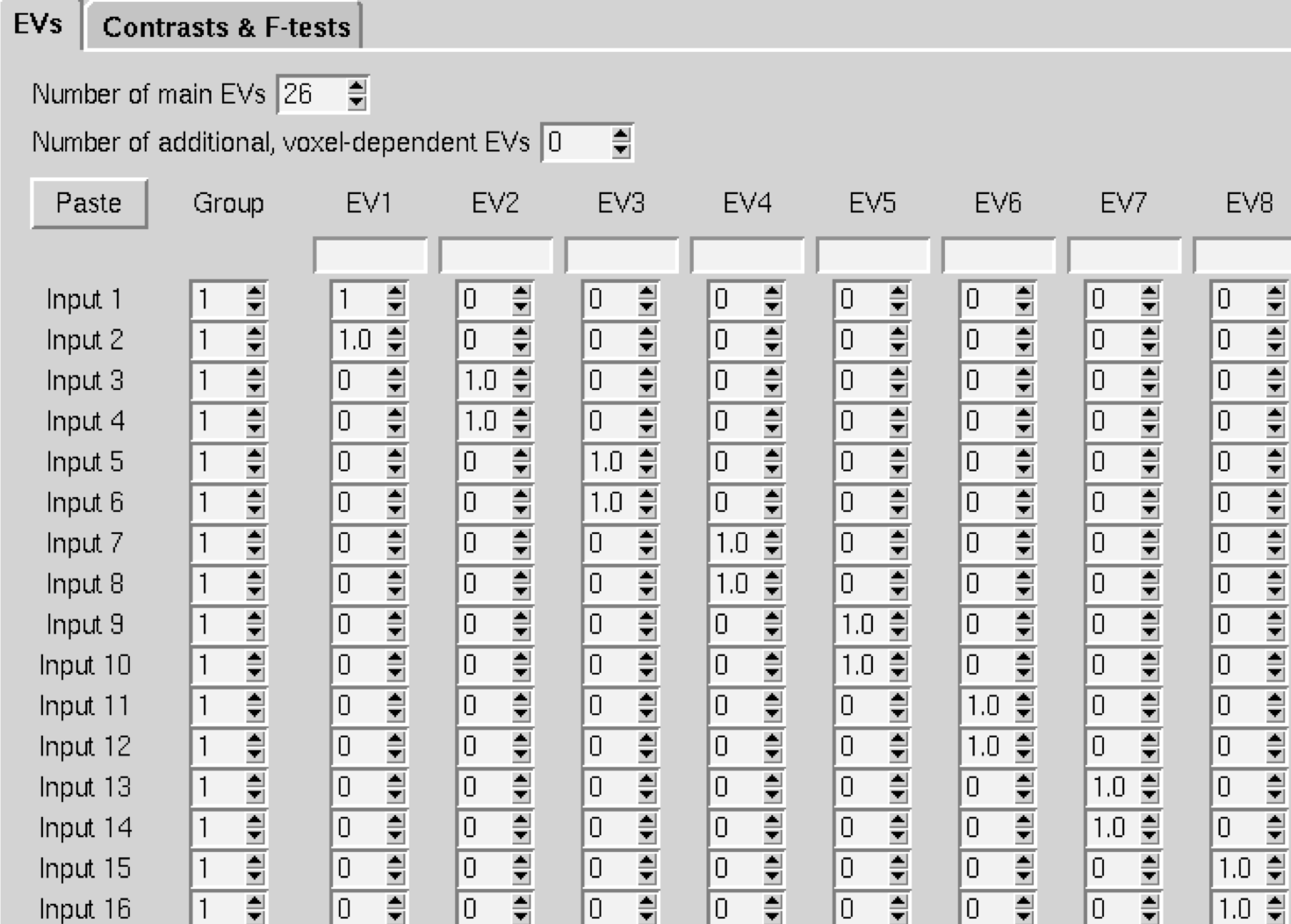
当我们完成后,点击Contrasts & F-tests标签,并将Contrasts的数量改为26。将对角线上的所有数字改为1;这将为每个受试者创建一个单一的对比度估计,即该受试者参数估计的平均值。
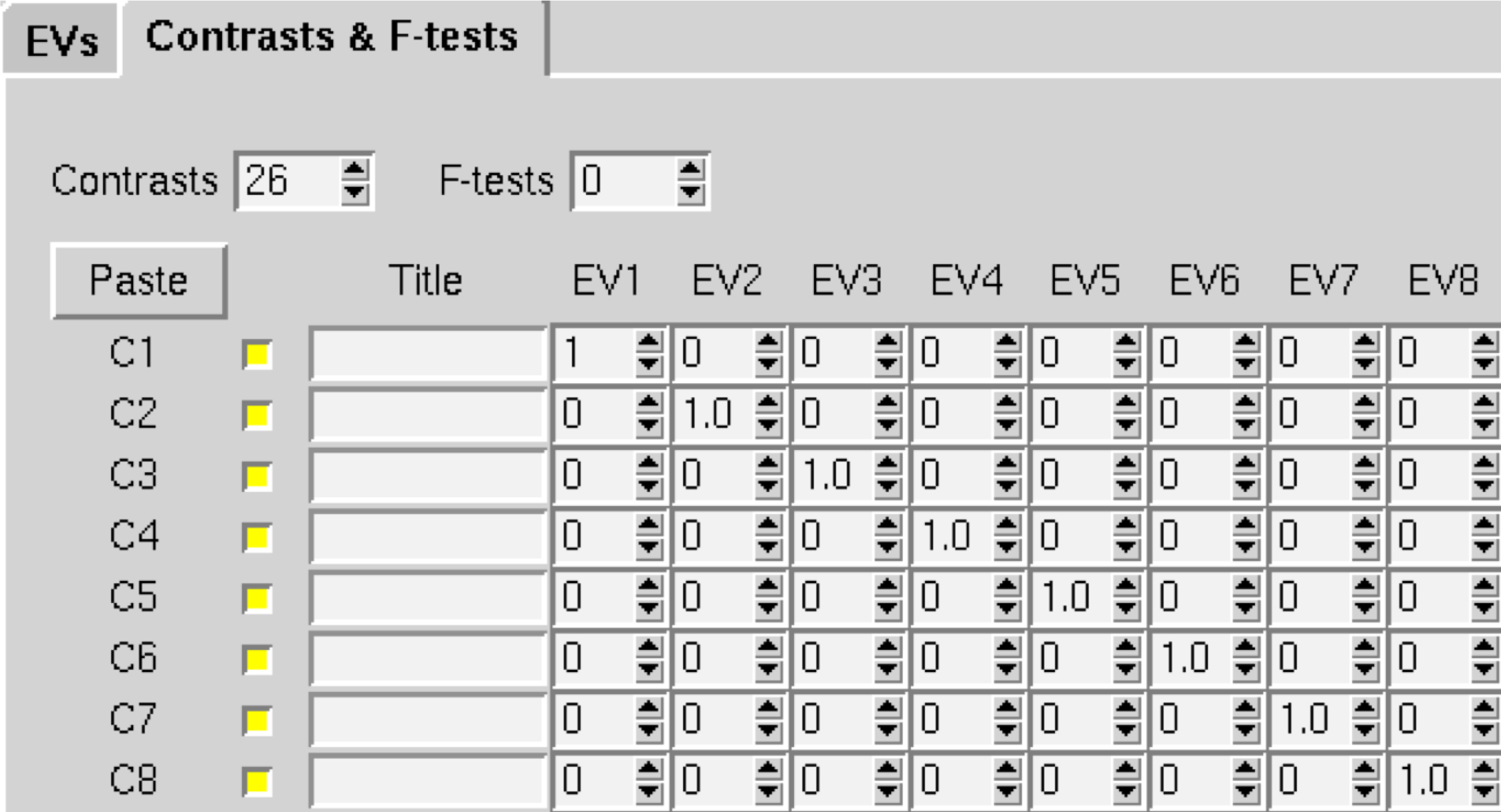
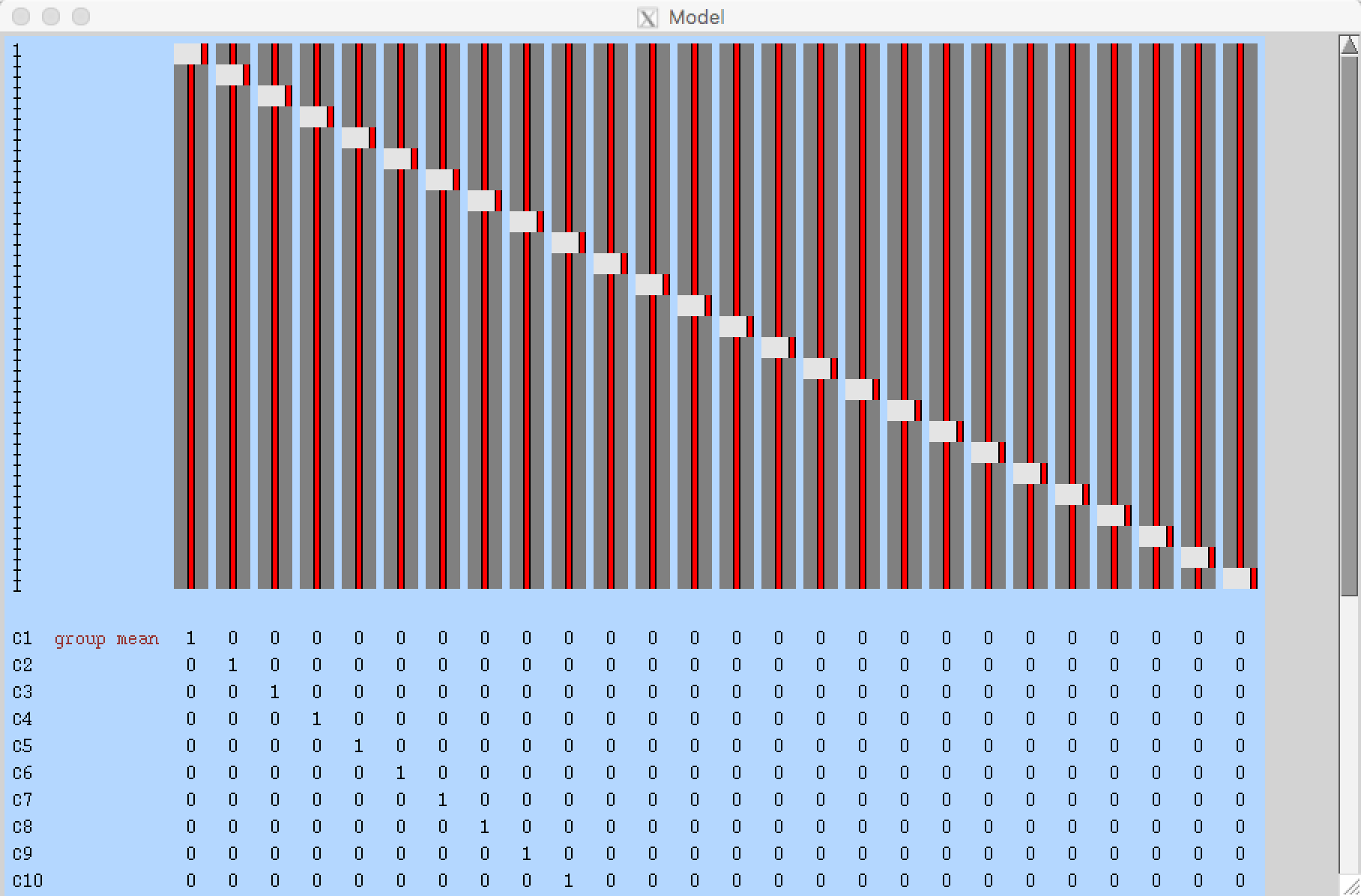
当完成了GLM和对比度的设置并点击Done后,应该看到像这样的东西:
与第一级分析一样,我们现在将忽略Post-stats标签,因为我们没有进行群体推断(population inference)。
第三级分析,3nd-Level Analysis
我们分析这个数据集的目的是将结果推广到样本所来自的人群。换句话说,如果我们在样本中看到大脑活动的变化,我们是否可以说这些变化也可能在人群中看到?
为了测试这一点,我们将进行第三级的分析。在FSL中,第三级分析是一个组水平分析–我们计算标准误差和对比估计值的平均值,然后测试平均估计值是否有统计学意义。
FSL一次只能运行一个模型。在这个例子中,我们将对 “Incongruent-congruent"的对比进行第三级的分析(在第二级的分析中被标记为cope3,因为它是被指定的第三个对比)。
加载数据
从Flanker目录中,打开FEAT图形用户界面(Feat_gui)。与第二级分析一样,选择更高级的分析(Higher-level analysis)。现在,不要选择FEAT目录,而是选择Inputs are 3D cope images from FEAT directories,并将输入的数量改为26。第二级分析产生了每个受试者的参数估计(或cope)的平均对比度,在我们的模型中指定的每个对比度。如同在第二层分析中选择FEAT目录一样,我们可以复制和粘贴cope图像的列表: 单击"Select cope images”,然后单击 “Paste"按钮。在终端中,导航到目录Flanker_2ndLevel.gfeat/cope3.feat/stats,并输入ls $PWD/cope* | sort -V。这将按数字顺序列出所有的cope图像,尽管它们没有被加零。通过键入ctrl+y将列表复制并粘贴到输入数据窗口。点击确定后,将输出目录标记为Flanker_Level3_inc-con。
创建GLM 点击 “Stats"选项卡。对于第三级分析,我们将使用混合效应(Mixed Effects)。这是对方差的建模,这样我们的结果就可以推广到我们的样本人群中。FLAME 1(FSL的混合效应局部分析)通过使用被试内和被试间变异性的信息来提供准确的参数估计;FLAME1+2被认为更准确,但额外的好处通常是最小的,而且过程要长得多。
最后一个选项,Randomise,使用非参数方法,当关于正态性的假设不成立时,它是有效的。稍后,我们将讨论为什么在某些情况下这是合适的。
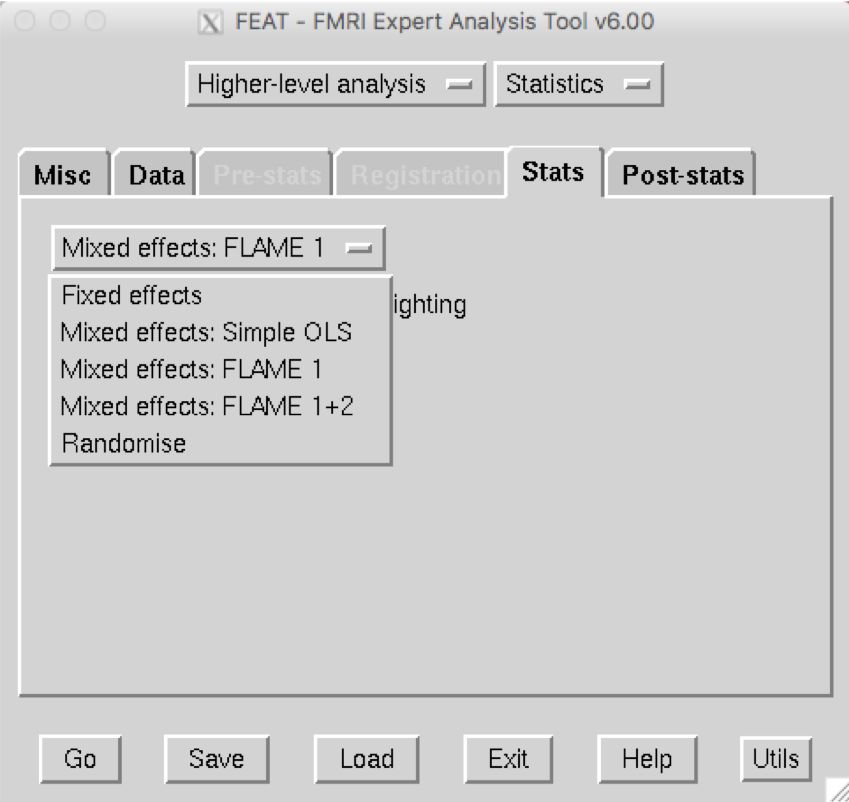 由于我们使用的是一个简单的设计,我们可以使用模型设置向导按钮(
由于我们使用的是一个简单的设计,我们可以使用模型设置向导按钮(Model setup wizard)快速创建一个GLM。我们已经提取了每个被试的对比度,所以我们可以选择单组平均(single group average)。当你点击处理(Process)时,应该看到一个模型表示,看起来像这样:

Post-Stats标签栏
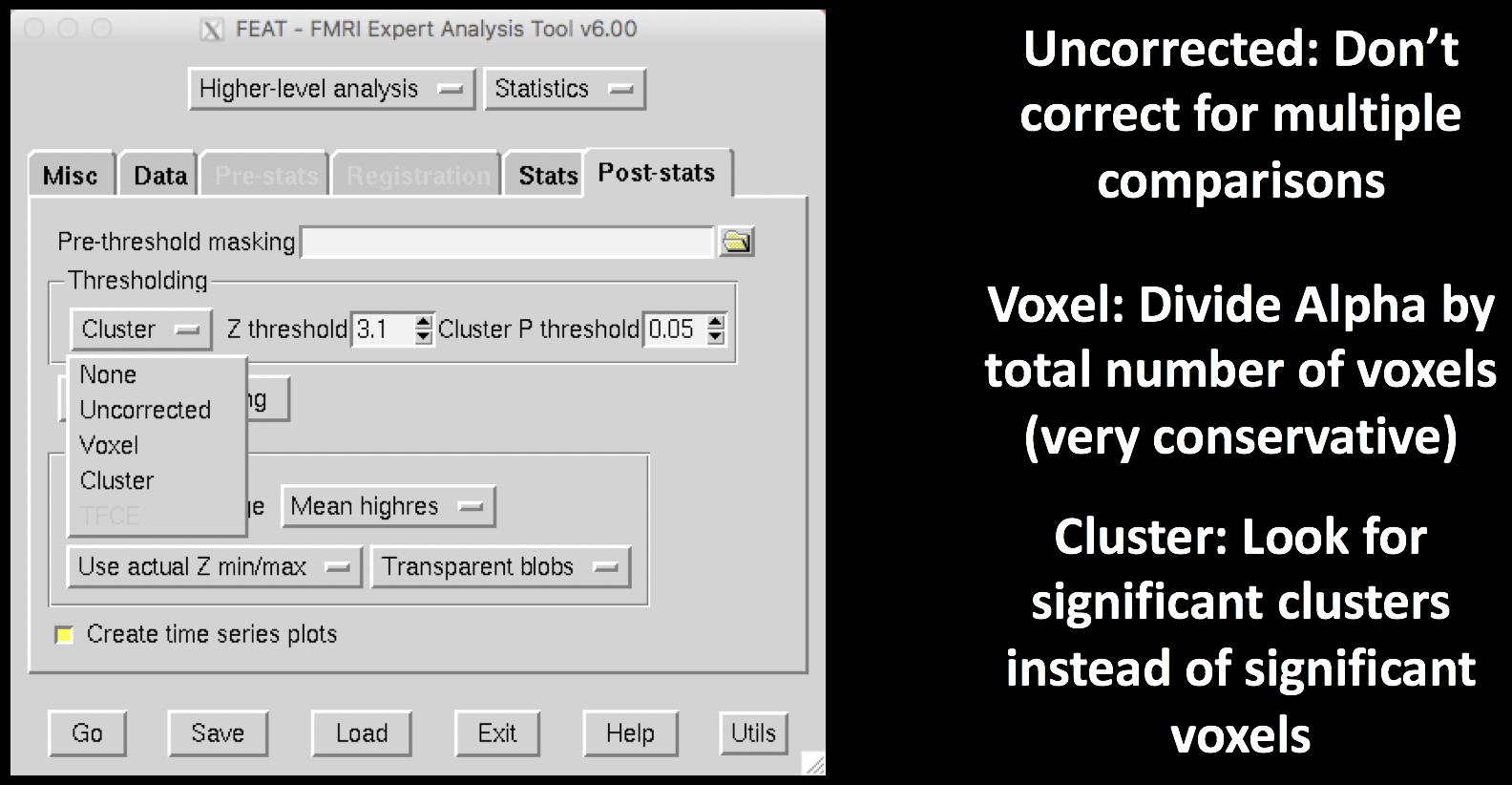
现在我们终于要讨论Post-Stats标签了。我们可能要考虑改变的唯一默认值是阈值(Thresholding)处理选项。None将不做任何阈值处理(即显示每个体素的参数估计值,无论其显著性如何);Uncorrected将允许任何单个体素通过Z-阈值中指定的阈值(例如、 这里我们只显示数值大于3.1的体素;Voxel将执行一种基于高斯随机场理论的最大高度阈值,它比Bonferroni检验更保守;最后是Cluster,它使用一个簇定义阈值(CDT,cluster-defining threshold)来确定一个体素簇是否有意义。这种方法背后的逻辑是,相邻的体素不是相互独立的,在估计显著性时要考虑到这种减少的自由度。
例如,如果我们把Z-阈值保持在3.1,而我们的集群p-阈值为0.05,我们将寻找由每个单独通过3.1的Z-阈值的体素组成的集群。FSL运行模拟,看看我们会有多大的集群,其每个组成体素都通过该z-阈值,并为该CDT创建一个集群大小的分布(类似于我们根据自由度计算t分布时的情况)。然后,在该CDT的模拟中出现少于5%的聚类大小被确定为显著。
对于大多数分析,默认的聚类校正分析,CDT为z=3.1,聚类阈值为p=0.05是合适的。关于不同软件包和不同聚类校正设置之间的假阳性率的详细比较,见Eklund等人2016年的原始论文;关于聚类校正的一些潜在问题的视频概述,请点击这里。
现在点击Go。这将需要大约5-10分钟,取决于你的电脑有多强大。
审查输出结果
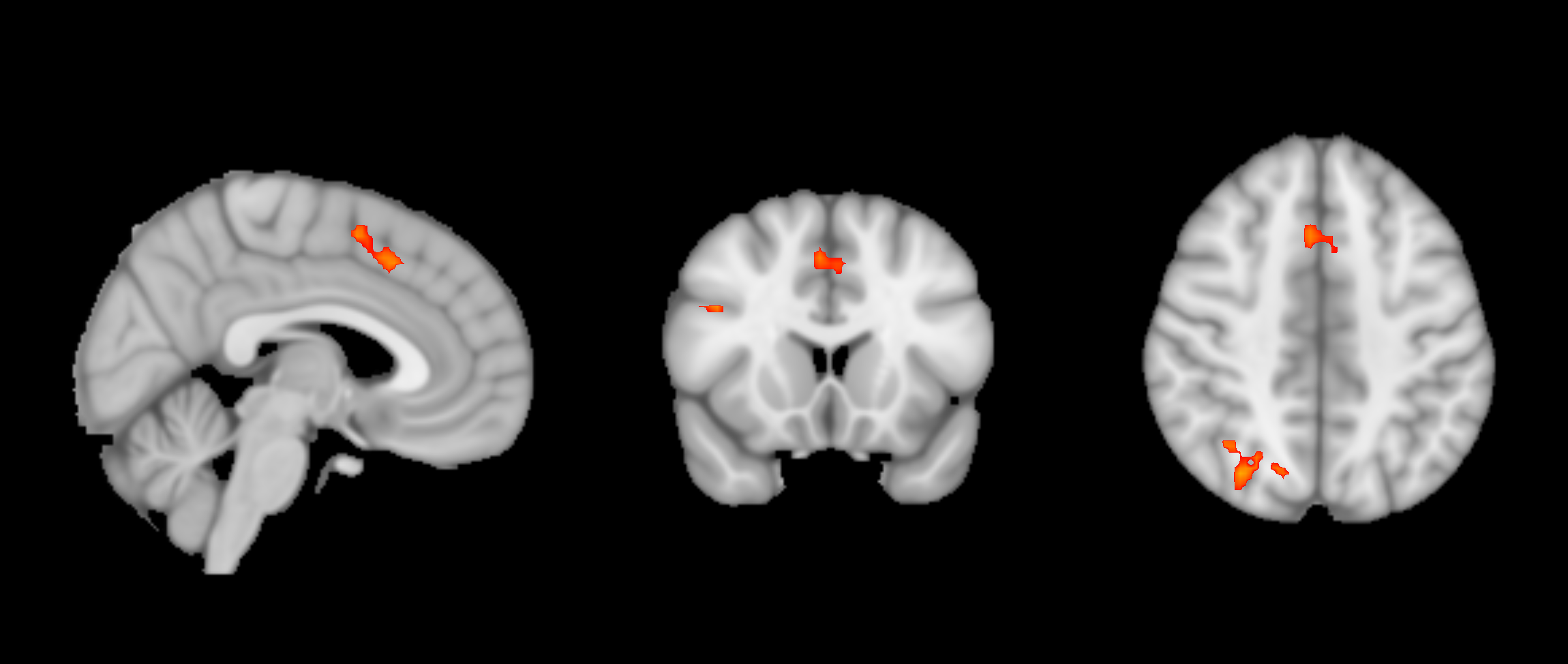
在FEAT的HTML输出中,你会看到阈值化的Z-统计学图像覆盖在MNI大脑模板上。这些是轴向切片,它们可以让你快速了解显著性簇的位置。
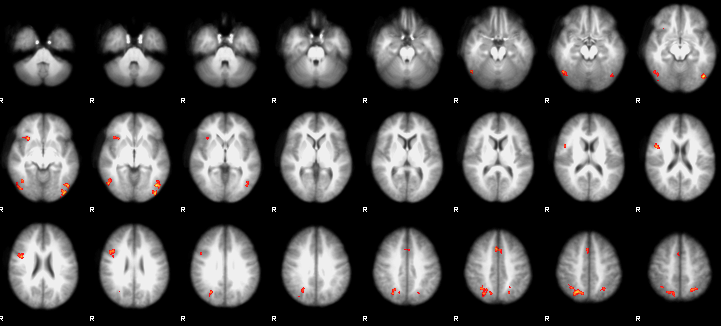
要仔细看一下结果,打开fsleyes并加载一个标准模板,比如MNI152_T1_1mm_brain(操作方法:点击标题栏的File > Add standard)。然后加载位于Flanker_3rdLevel_inc-con.gfeat/cope1.feat的thresh_zstat1.nii.gz图像。这个图像只显示那些根据你在Post-stats标签中指定的标准被确定为显著性簇。
为了使结果看起来更干净,把颜色方案改为 “Red-Yellow”,并把 “Min.“值改为3.1。你也可以点击齿轮图标,改变插值,使结果看起来更平滑。最后,点击背内侧前额叶皮层区域(dorsal medial prefrontal cortex area)的一个簇,并通过点击十字线图标关闭十字线。(这些都是外观上的选择,你可以随心所欲地改变它们。)然后可以用相机图标对这个蒙太奇进行快照,并在你的手稿中使用。