FSL系列教程 #4. ROI分析
简介
我们刚刚完成了一个组分析,并确定了大脑的哪些区域在实验的不一致(“Incongruent”)和一致(“congruent”)条件下显示出明显的差异。对于一些研究人员来说,这可能是他们想要做的全部。
这种分析被称为全脑(whole-brain)或探索性分析(exploratory)。当实验者对差异的位置没有假设时,这些类型的分析很有用;这个结果将作为未来研究的基础。
然而,当对一个特定的被试进行了大量的研究后,我们可以开始对我们应该在大脑图像中找到的结果做出更具体的假设。例如,认知控制已经被研究了很多年,许多关于它的fMRI研究已经发表,使用不同的范式,将认知要求较高的任务与认知要求较低的任务进行比较。通常情况下,在认知要求高的条件下,BOLD信号的明显增加出现在大脑的一个区域,即背内侧前额叶皮层(dosal medial prefrontal cortex),或简称为dmPFC。那么,对于Flanker研究,我们可以将我们的分析限制在这个区域,只从该区域的体素中提取数据。这就是所谓的兴趣区域(ROI,region of interest)分析。在看全脑结果之前,选择分析一个选定的区域,这种分析的一般名称叫做确认性分析(confirmatory analysis)。
全脑图(Whole-brain maps)可以隐藏我们正在研究的效果的重要细节。我们可能会发现incongruent-congruent的显着效应,但效应显着的原因可能是incongruent大于congruent,或者是incongruent比congruent的消极得多,或者是两者的某种组合。确定是什么在驱动这种效应的唯一方法是ROI分析,这在处理交互作用和更复杂的设计时尤其重要。
使用脑图谱
为我们的ROI分析创建一个区域(region)的方法是使用图谱(atlas),或将大脑划分为解剖学上的不同区域的地图。
FSL已经安装了许多图谱(atlas),我们可以通过FSL viwer访问这些图谱。如果点击 “Settings”->“Ortho View 1”->“Atlas Panel”,就会打开一个名为Atlases的新窗口。默认情况下,将加载哈佛-牛津大学皮质和皮质下图谱(Harvard-Oxford Cortical and Subcortical Atlases)。我们可以通过点击图谱名称旁边的Show/Hide链接看到图集是如何分割大脑的。观察窗口中十字线中心的体素将被分配一个属于大脑结构的概率。
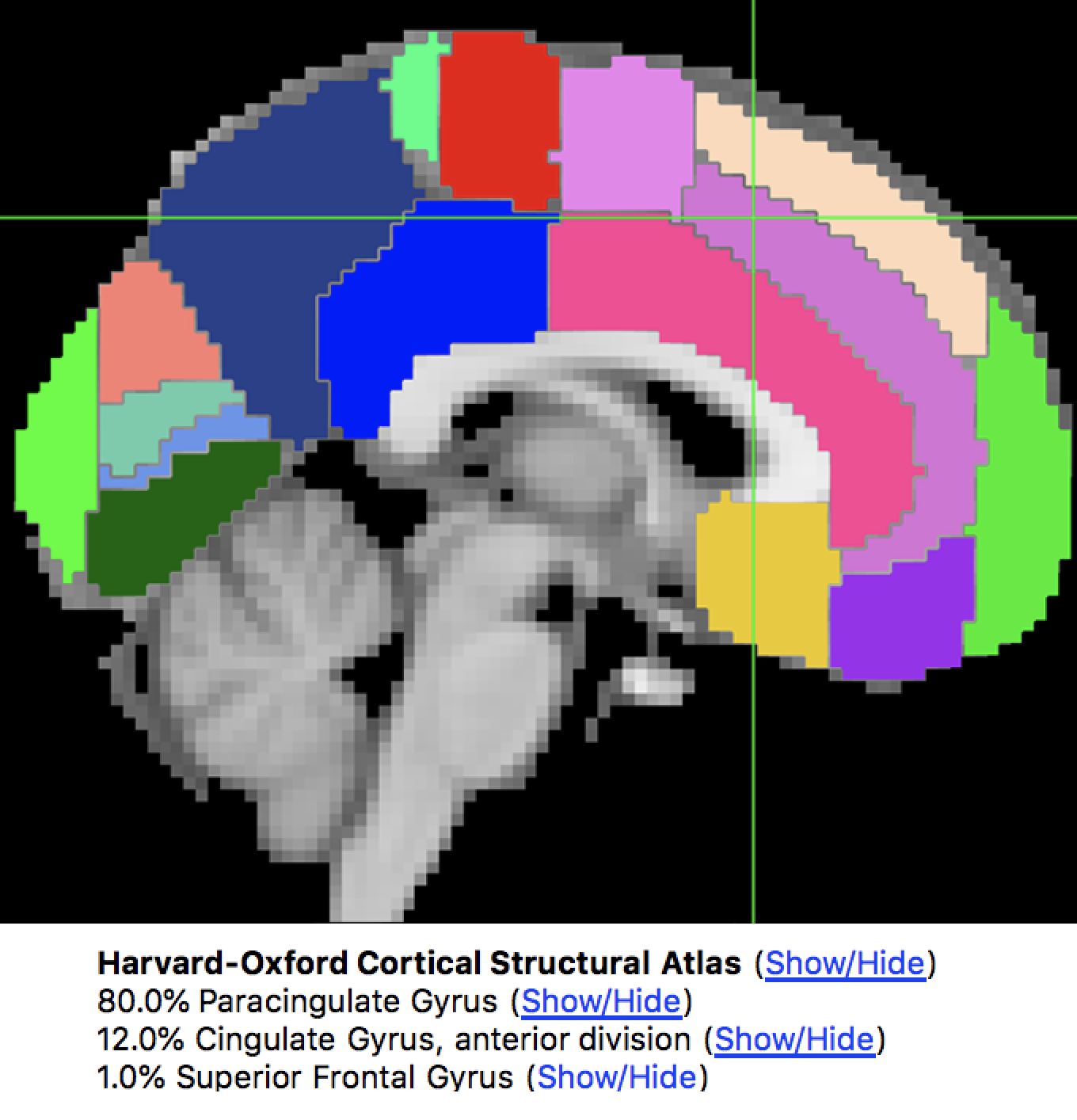
要将这些区域之一保存为提取数据的文件,也称为掩膜(mask),点击想用作mask的区域旁边的Show/Hide链接–在我们的例子中,假设我们想用副扣带回(Paracingulate Gyrus)作为mask。点击该链接将显示该区域叠加在大脑上,并在 “Overlay list"叠加列表窗口中将其加载为叠加。点击图像旁边的磁盘图标,将其保存为一个mask。把它保存到Flanker目录下,称为PCG.nii。
我们的结果将具有与我们用于归一化的模板相同的分辨率。FSL中默认的是MNI_152_T1_2mm_brain,它的分辨率为2x2x2mm。当我们创建一个mask时,它的分辨率将与它所覆盖的模板相同。当我们从mask中提取数据时,数据和mask需要有相同的分辨率。为了避免因图像分辨率不同而导致的任何错误,请使用与我们用于归一化数据的相同模板来创建mask。
使用结构像掩膜抽取数据
一旦创建了掩膜,我们就可以从中提取每个受试者的对比度估计值(contrast estimates)。虽然你可能认为我们会提取第三级分析的结果,但实际上我们想要的是第二级分析的结果;第三级分析是一个单一的图像,每个体素都有一个数字,而在ROI分析中,我们的目标是单独提取每个受试者的对比度估计。
以Incongruent-Congruent对比度估计为例,我们可以在Flanker_2ndLevel.gfeat/cope3.feat/stats目录下找到每个受试者的数据图(data maps)。这些数据图有几种不同的计算方式,包括t统计图、cope图和方差图。我更倾向于从z-统计图中提取数据,因为这些数据已经被转换为正态分布的形式,在我看来,更容易绘制和解释。
为了使我们的ROI分析更容易,我们将把所有的z-统计图合并成一个数据集。为了做到这一点,我们将使用FSL命令和Unix命令的组合。导航到Flanker_2ndLevel.gfeat/cope3.feat/stats目录,然后输入以下内容:
fslmerge -t allZstats.nii.gz `ls zstat* | sort -V`
这将沿着时间维度(用-t选项指定)把所有的Z-statistic图像合并成一个数据集;这只是意味着把各volume数据串联起来,成为一个更大的数据集。第一个参数是输出数据集的名称(allZstats.nii.gz),后面的代码使用星号通配符列出每个以 “zstat"开头的文件,然后用-V选项从小到大对它们进行数字排序。
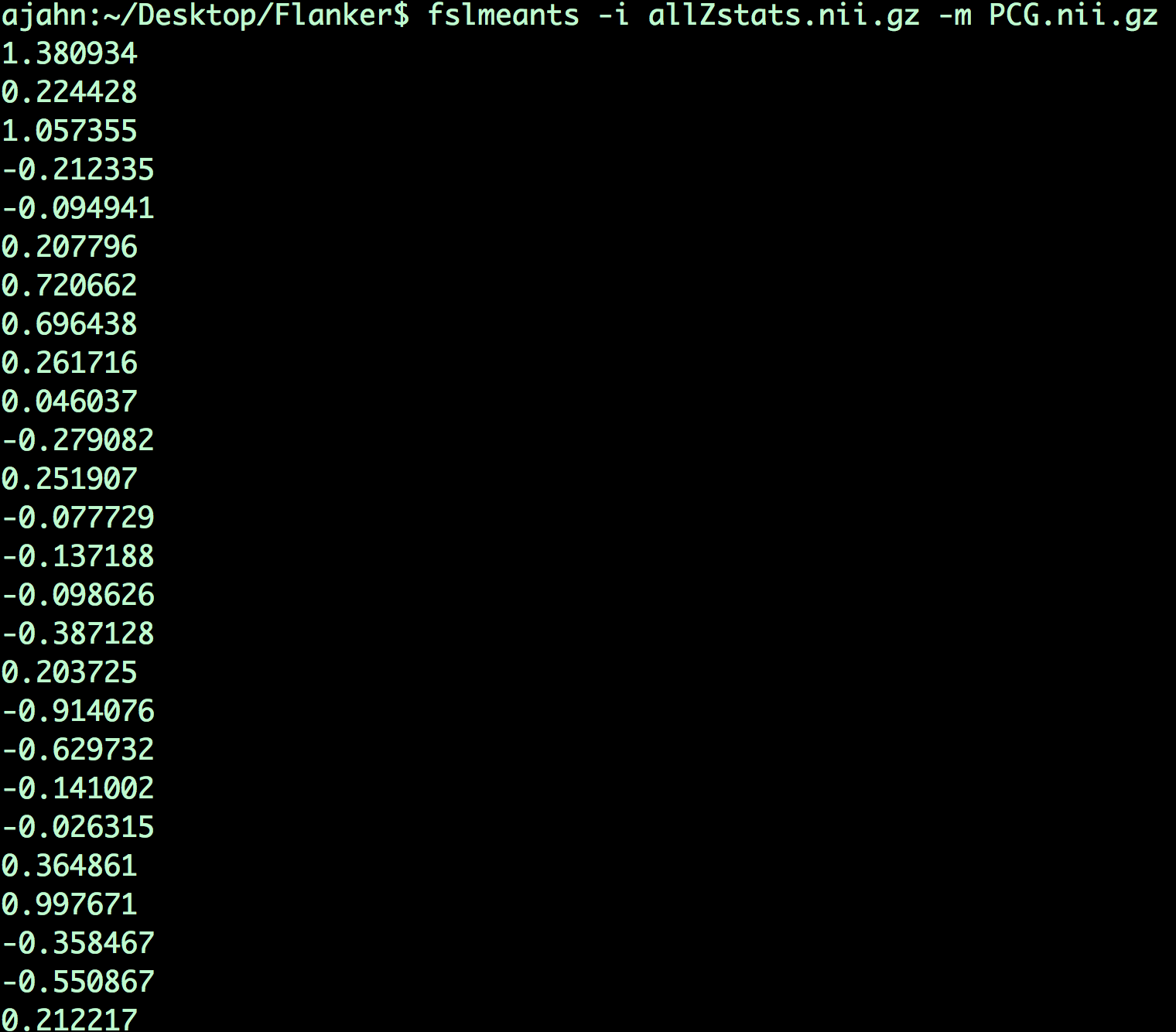
将allZstats.nii.gz文件上移三层,使其位于Flanker主目录中(即输入mv allZstats.nii.gz .../../...)。然后使用fslmeants命令从PCG掩码中提取数据:
fslmeants -i allZstats.nii.gz -m PCG.nii.gz
这将打印26个数字,每个被试一个。每个数字是该被试的对比度估计值,是mask中所有体素的平均数。
使用球体抽取数据
我们可能已经注意到,使用解剖学掩膜的ROI分析结果并不显著。这可能是因为PCG掩膜覆盖了一个非常大的区域;虽然PCG被标记为一个单一的解剖区域,但我们可能是从几个不同的功能区域提取数据。因此,这可能不是最好的ROI方法。
另一种技术被称为球形ROI方法(spherical ROI)。在这种情况下,一个给定直径的球体以指定的X、Y和Z坐标的三组为中心。这些坐标通常是基于另一项研究的峰值激活,该研究使用与我们所使用的相同或相似的实验设计。这被认为是一个独立的分析,因为ROI的定义是基于一个单独的研究。
下面的动画显示了解剖学和球形ROI的区别:

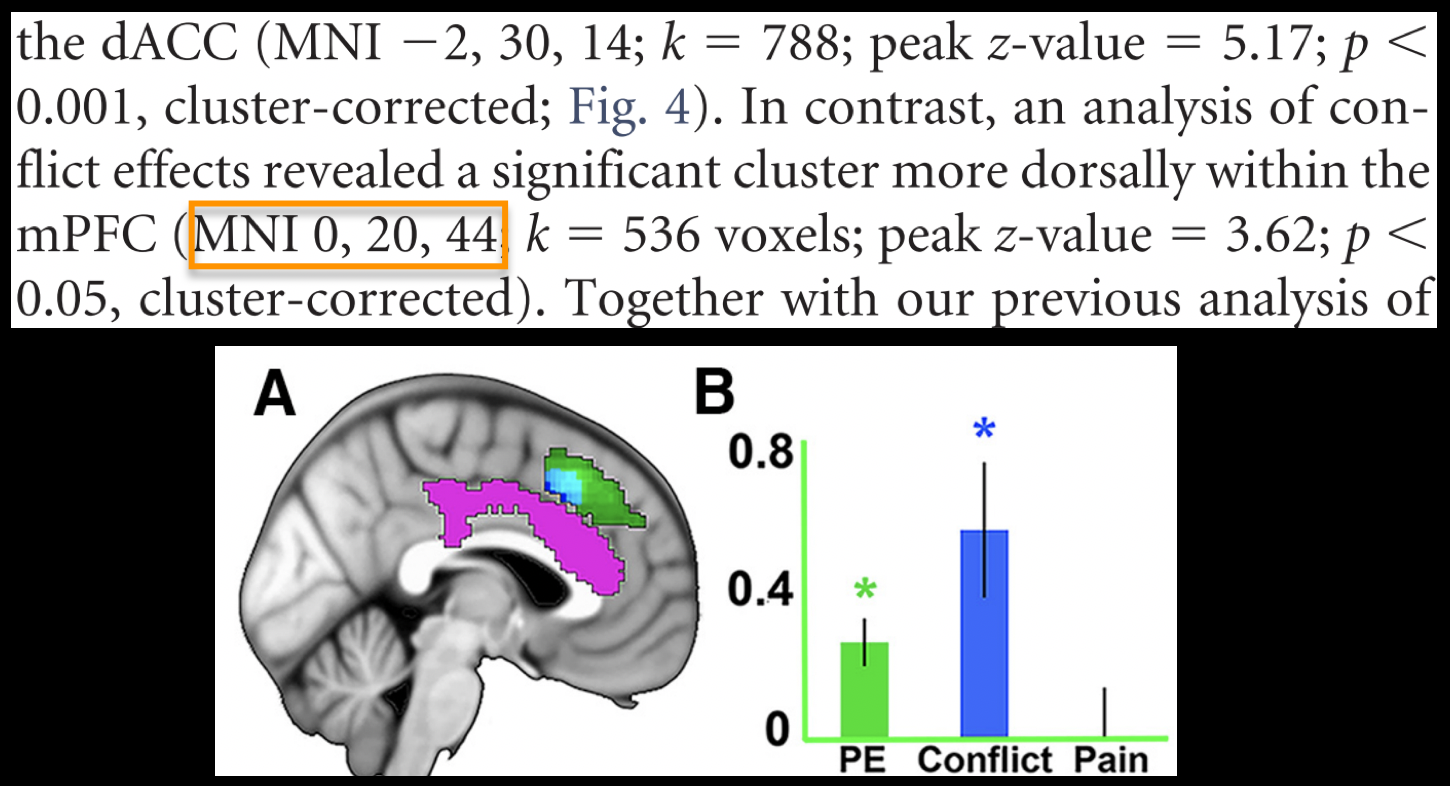
为了创建这个ROI,我们需要从另一项研究中找到峰值坐标;让我们随机挑选一篇论文,如Jahn等人,2016。在结果部分,我们发现Stroop任务存在冲突效应–这是一个不同但相关的实验设计,也是为了挖掘认知控制–在MNI坐标0、20、40处有一个峰值t统计。
接下来的几个步骤很复杂,所以要密切注意每一个步骤:
-
打开fsleyes,并加载一个MNI模板。在
Location窗口的"Coordinates:MNI152"“下的字段中,输入0 20 44。就在这些字段的右边,注意体素位置下的字段中的数字的相应变化。在这种情况下,它们是45 73 58。写下这些数字。 -
在终端中,导航到Flanker目录并输入以下内容:
fslmaths $FSLDIR/data/standard/MNI152_T1_2mm.nii.gz -mul 0 -add 1 -roi 45 1 73 1 58 1 0 1 Jahn_ROI_dmPFC_0_20_44.nii.gz -odt float
这是一条长而密集的命令,但现在只需注意我们在哪里插入了数字45、73和58。当我们根据不同的坐标创建另一个球形ROI时,这些是我们唯一要改变的数字。(当你创建一个新的ROI时,你也应该改变输出文件的标签)。这个命令的输出是一个单一的体素,标志着上述指定坐标的中心。
- 接下来,键入
fslmaths Jahn_ROI_dmPFC_0_20_44.nii.gz -kernel sphere 5 -fmean Jahn_Sphere_dmPFC_0_20_44.nii.gz -odt float
这就把单个体素扩展成一个半径为5毫米的球体,并调用输出"Jahn_Sphere.nii.gz”。例如,如果想把球体的大小改为10毫米,你可以把这部分代码改为-kernel sphere 10。
- 现在,输入
fslmaths Jahn_Sphere_dmPFC_0_20_44.nii.gz -bin Jahn_Sphere_bin_dmPFC_0_20_44.nii.gz
这将对球体进行二进制化处理,从而使其能够被FSL命令所读取。
在刚才列出的步骤中,注意到每个命令的输出是如何作为下一个命令的输入的。如果你决定创建一个ROI,你将为你自己的ROI改变这一点。
- 最后,我们将从这个ROI提取数据,键入:
fslmeants -i allZstats.nii.gz -m Jahn_Sphere_bin_dmPFC_0_20_44.nii.gz
你从这个分析中得到的数字应该与你用解剖掩码创建的数字大不相同。将这些命令复制并粘贴到你选择的统计软件包中,并对其进行单样本t检验。它们有意义吗?如果你要在手稿中写出这些结果,你会如何描述它们?
练习实践
fslmeants使用的掩码是二进制的,这意味着任何含有大于0的数值的体素将被转换成 “1”,然后只从那些标有 “1 “的体素中提取数据。你会记得,用fsleyes创建的掩码是概率性的。如果你想用概率权重对提取的对比度估计值进行加权,你可以通过使用fslmeants的-w选项来实现。试着输入
fslmeants -i allZstats.nii.gz -m PCG.nii.gz -w
并观察数字与之前使用二进制掩码的方法有什么不同。差异小吗?大吗?这是你所期望的吗?
- 使用球状ROI分析部分给出的代码,创建一个半径为7毫米的球体,位于MNI坐标36, -2, 48。
- 使用哈佛-牛津大学皮层下图谱创建一个右杏仁核的解剖掩膜。按你想要的方式给它贴上标签。然后,从应付1中提取z统计数字(即与基线相比,Incongruent的对比估计)。